Physique des chocs.
Concours interne d'ingénieur de l'industrie et des mines
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Pendule de Newton.
ce pendule est constitué de cinq billes d'acier suspendues à un bâti.
Les cinq pendules sont identiques et au repos les billes sont en
contact. En écartant la bille n°1 à la main puis en l'abandonant on
observe un transfert périodique de mouvement de la bille 1 à la bille
5, les billes intermédiaires restant immobiles.
Justifier cette expérience.
Il s'agit d'une collision élastique frontale à une dimension. Les billes ont toute la même masse m.
On note v0 la vitesse initiale de la bille n°1, v1 sa vitesse après le choc et v2, la vitesse de la bille n°5 après le choc.
Conservation de la quantité de mouvement du système constitué par les cinq billes :
mv0+ 0 = mv1 +mv2 ; v0 = v1 +v2 (1)
Conservation de l'énergie cinétique de ce même système :
mv02 = mv12 +mv22 ; v02 = v12 + v22 (2).
Elever (1) au carré : v02 = v12 + v22 +2v1v2.
2v1v2 = 0 ; v1 = 0 et v2 = v0.
La bille n°1 s'arrète ; la bille n°5 possède l'énergie cinétique initiale ½mv02 et la quantité de mouvement mv0.
Canon de Gauss.
Un rail sert de guide de roulement à des billes d'acier. De petits aimants, cylindriques ont la même taille que les billes.
On forme sur le rail des "étages" comportant un aimant suivi de deux
billes. Une bille est lancée à faible vitesse vers l'étage 1. Elle est
attirée progressivement et heurte l'aimant. A la manière d'un pendule
de Newton, la dernière bille de cet étage décolle avec une vitesse non
négligeable et vient percuter l'aimant de l'étage suivant. Le phénomène
se reproduit d'étage en étage si bien que la dernière bille est
propulsée à grande vitesse.
Quelle est le signe de l'énergie potentielle magnétique entre un aimant et une bille d'acier ?
Si l'aimant et la bille sont suffisamment éloignés, l'énergie du système bille + aimant est nulle.
Lorsque la bille se rapproche de l'aimant elle possède une énergie cinétique Ec positive. La conservation de l'énergie du système donne : Ec + Epotentielle magnétique =0.
L'énergie potentielle magnétique est négative.
Pourquoi
la position des billes dans la situation finale correspod à une énergie
potentielle inférieure à celle de la position initiale ?
L'énergie mécanique du système se conserve et une partie de l'énergie potentielle magnétique est convertie en énergie cinétique.
Quelle valeur maximale peut-on attribuer à l'énergie cinétique acquise par la dernière bille ?
L'énergie cinétique initiale de la bille est négligeable ; la
conservation de l'énergie indique que l'énergie cinétique maximale de
la dernière bille est égale à l'énergie potentielle magnétique de tous
les aimants.
Dipole magnétique.
Un dipole magnétique placé en O crée au point P un champ magnétique propre.
En déduire le champ magnétique crée par ce dipôle si le point P est à l'abscisse x sur Ox.

|
| .
. |
|
|
Ce dipole placé dans un champ magnétique extérieur possède une énergie potentielle magnétique Emag.
Quelle est la force magnétique sur ce dipôle ?
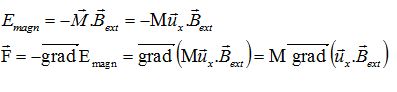
Le moment magnétique aquis par une sphère d'acier placé dans un champ magnétique est donné par la formule empirique 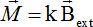 avec k constante positive. avec k constante positive.
Estimer l'expression de l'énergie cinétique maximale acquise par la dernière bille si il y a 4 étages.
Diamètre des billes = largeur des aimants = s2R.
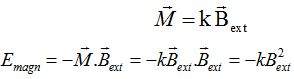
A chaque étage, l'énergie cinétique maximale est égale, en valeur absolue, à l'énergie potentielle magnétique.
|
.
|
|
Canon électromagnétique.
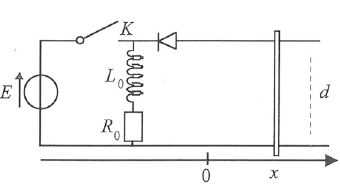
On considère deux rails parallèles de longueur D, écartés d'une
distance d et reliés par un barreau mobile de masse m. On note L(x)= l
x l'inductance du dispositif, la résistance des rails étant nulle.
Initialement, le mobile est au repos en x=0, l'interrupteur K étant
fermé. Lorsqu'il circule un courant I0 constant dans R0, on ouvre K et il passe un courant i(t) dans le barreau.
Expliquer en quoi ce dispositif peut servir de propulseur pour le barreau.
K fermé : la bobine inductive stocke de l'énergie magnétique ½L0I02; la diode est non passante.
A l'ouverture de l'interrupteur, cette bobine cède son énergie :
Energie fournie au circuit et au projectile par l'inductance de stockage L0 = énergie cinétique du projectile + énergie stockée par autoinduction dans les rails + énergie dissipée par effet Joule.
La variation d'énergie magnétique se retrouve sous forme d'effet Joule dans R0 et d'énergie cinétique au barreau.
Le barreau est placé dans le champ magnétique B = k i(t) ( avec k une
constante) crée par le courant i(t), le barreau est soumis à une force
de Laplace F = B i(t) d = constante i2(t).
D'après la loi de Lenz, une fem apparaît aux bornes du barreau ; celle-ci s'oppose à la diminution de l'intensité du courant.
D'après la loi de Faraday, le flux du champ magnétique induit doit
augmenter : ce qui implique d'augmenter la surface du circuit.
Donner l'équation électrique du circuit. On pose L = L0 + lx.
K ouvert : d(Li)/dt +R0 i = 0 ; Ldi/dt + idL/dt +R0 i = 0 ; (L0+ l x )di/dt + l i dx/dt + R0 i = 0.
A partir de l'énergie magnétique montrer que le barreau est soumis à la force F = ½l i2.
Puissance mise en jeu en sus de la puissance Joule ( F = L i(t) flux propre) : P = i(t) dF/dt = i2(t) dL/dt + L i(t) di(t) / dt.
Cette puissance correspond à la variation d'énergie magnétique Em et à la puissance Pméca de la force de Laplace : P = dEm/dt + Pméca.
Pméca = P-dEm/dt avec Em = ½Li2(t) ; dEm/dt = L i(t) di(t) / dt + ½i2(t)dL/dt.
Pméca = i2(t) dL/dt + L i(t) di(t) / dt - L i(t) di(t) / dt - ½i2(t)dL/dt = ½i2(t)dL/dt.
dL/dt = d(L0 + lx) /dt =l dx/dt et Pméca = F v = F dx/dt.
F dx/dt = ½i2(t)dL/dt = ½i2(t)l dx/dt ; F = ½i2(t)l .
Pour L0 >> lD, exprimer la vitesse maximale du barreau.
m=30 kg ; L0 = 1 H ; l = 4 10-7 H m-1 ; R0 = 0,01 ohm ; E = 3 kV.
En régime permanent, K fermé : I0 = E/R0 = 3 103 / 0,01 = 3,0 105 A.
Energie stockée par la bobine : ½L0I02 = 0,5*1*(3,0 105)2 =4,5 1010 J.
Si L0 est suffisamment importante, l'intensité dans le circuit diminue peu et i(t) ~I0.
Temps caractéristique t de la décroissance de l'intensité : t ~ L0 / R0 ~1/0,01 ~ 100 s.
Equation mécanique, la seule force qui intervient étant la force de Laplace : m x" = ½l i2~½l I02 ; x"~l I02/(2m) =(3,0 105)2 *4 10-7 /60 =6 102 m s-2.
vitesse : x' = x"t + v0 avec v0 = 0 ( barre initialement immobile ).
x'(t=1) = 6 102 m/s.
Distance parcourue : ½x"t2 ; x(t=1) = 300 m.
|
|
|

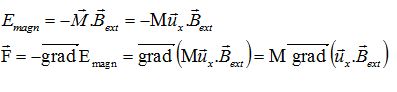
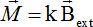 avec k constante positive.
avec k constante positive.