Identification d'un liquide par mesure de l'indice de réfraction. Concours général 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Le composé A2, appelé usuellement acide méthacrylique, est à température ambiante, un liquide incolore d'odeur âcre de température de fusion Tf = 14°C et de température d'ébullition Teb =162°C. On peut donc l'identifier en mesurant son indice de réfraction à l'aide d'un réfractomètre d'Abbe. Cet appareil mesure l'angle de réfraction i2 d'un rayon lumineux qui est relié à l'angle d'incidence i1 selon les lois de Snell-Descartes. Le dioptre considéré est l'interface formée par la substance S dont on veut déterminer son indice de réfraction ns et le prisme P qui a un indice de réfraction np élevé ( np > ns). 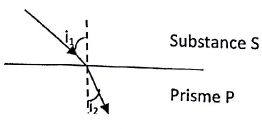Donner la loi de Snell-Descartes relative à la réfraction, liant i1, i2, ns et np. ns sin i1 = np sin i2. En réalité pour observer le rayon réfracté, il s'avère indispensable d'utiliser un système optique tel qu'une lunette et un oculaire. les rayons lumineux doivent donc traverser l'interface prisme-air, induisant ainsi un autre changement de direction des rayons lumineux au niveau de ce nouveau dioptre. A quelle condition sur i y aura-t-il un faisceau émergeant ? On cherchera une inégalité entre i1, nair, np, ns et A. 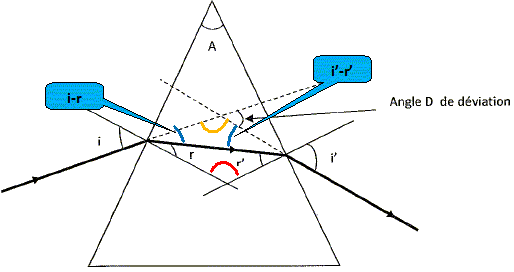Réfraction sur le dioptre substance-prisme : ns sin i = np sin r soit r = sin-1(ns sin i / np ). Réfraction sur le dioptre prisme-air : np sin r' = nair sin i'. sin i' doit être inférieur ou égal à 1 soit : sin r' <=nair / np. La somme des angles r+r' et l'angle A ont le même supplément ( l'angle noté en rouge) : A = r+r'. sin (A-r) <= nair / np soit A-r <= sin-1(nair / np). A-sin-1(ns sin i / np ) <=sin-1(nair / np). .. .. Sachant que np =1,7, ns =1,3, A = 61,0° et nair = 1,0, calculer la valeur minimum de l'angle d'incidence i1, pour qu'il existe  un faisceau émergeant du prisme. 61,0-sin-1(1,3 sin i1 / 1,7 ) <= sin-1(1,0 / 1,7). 61,0-sin-1(1,3 sin i1 / 1,7 ) <= 36,03 ; 61,0-36,03 <= sin-1(0,765 sin i1 ). 24,97 <= sin-1(0,765 sin i1 ) ; 0,4221 <= 0,765 sin i1 ; sin i1 >= 0,552 ; i1 > = 33,5°. . Dans le réfractomètre d'Abbe, l'angle d'incidence i1 est de 90° ; on dit que le rayon lumineux arrive sous incidence rasante. Déterminer la relation permettant de calculer i2 en fonction des indices ns et np. Réfraction sur le dioptre substance-prisme : ns sin 90 = np sin r soit r = sin-1(ns / np ). Réfraction sur le dioptre prisme-air : np sin r' = nair sin i2. A = r+r' ; np sin (A-r) = nair sin i2 soit A-r <= sin-1(nair / np sin i2). A-sin-1(ns / np ) = sin-1(nair / npsin i2). Le réfractomètre d'Abbe est constitué d'un prisme d'angle au sommet A = 61° et d'indice de réfraction np =1,7. On dépose une goutte de substance à analyser sur le prisme et la mesure de l'angle de réfraction i' permet de déterminer ns. On mesure i' = 6,4°. 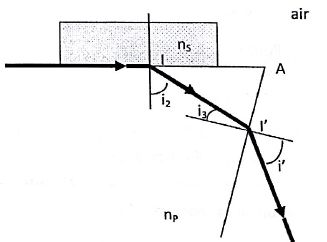Déterminer la relation entre i2, i3 et A. i2+i3 d'une part, A d'autre part, ont le même suplément : A =i2+i3. En déduire l'expression de i3 en fonction de A, ns et np. ns sin 90 = np sin i2 ; i2 = sin-1( ns /np) ; A =sin-1( ns /np) +i3 ; i3 =A -sin-1( ns /np). Donner la relation entre i' et i3, et enfin entre i', A, np et ns. En déduire la valeur de ns. np sin i3 = nair sin i' = sin i' ;  i' = sin-1(np sin i3) ; i' = sin-1(np sin (A -sin-1( ns /np))). 6,4 = sin-1(1,7 sin (61,0 -sin-1( ns /1,7))). sin 6,4 =1,7 sin (61,0 -sin-1( ns /1,7)) ; 0,06557 =sin (61,0 -sin-1( ns /1,7)). 3,76 = 61,0 -sin-1( ns /1,7) ; sin-1( ns /1,7) =57,24 ; ns /1,7 =0,841 ; ns =1,43 ~1,4.

menu