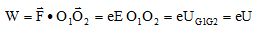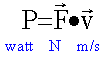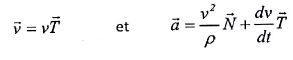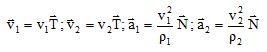Spectrographe de masse. Concours général 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Dans un spectrographe de masse, les molécules organiques en phase gazeuse sont bombardées par un flux d'électrons. Des ions positifs sont formés et séparés en fonction de leur masse. La formule moléculaire exacte est déterminée à partir de la masse de ces ions. Un spectrographe de masse est constitué de plusieurs parties comme l'indique la figure ci-dessous : 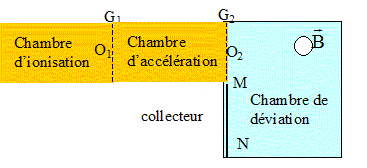Dans la chambre d'ionisation sous l'effet d'un bombardement électronique, l'acide crotonique est fragmenté, ionsé en cations de charge q = +e. On s'intéresse ici à deux de ces ions de masses respectives m1 et m2. En O1 la vitesse de es ions est négligeable. Les ions sont accélérés entre O1 et O2 sous l'action d'un champ électrique uniforme E créé par une différence de potentiel U = VG1-VG2. Dans la chambre de déviation, ces ions sont déviés par un champ magnétique uniforme de direction perpendiculaire au plan de la figure et venant vers nous. Un collecteur d'ions est constitué d'une plaque photosensible entre M et N. Les chambres sont sous vide. On négligera le poids devant les autres forces. Donner l'expression de la force électrostatique F s'exerçant sur un ion de charge e. Comment doit être orienté ce champ pour qu'il y ait accélération dans la chambre (2) ? Signe de la différence de potentiel VG1-VG2 pour que les ions soient accélérés entre O1 et O2 : th. de l'énergie cinétique entre G1 et G2 : le poids est négligeable devant la force électrique. le travail de la force électrique est : q (VG1-VG2) ; ce travail doit être moteur pour que les ions soient accélérés : or q=e, charge positive des ions, donc VG1-VG2 positive. Le champ E0 pointe vers le plus petit potentiel, donc vers G2. La charge étant positive, le champ et la force électriques sont colinéaires et de même sens. 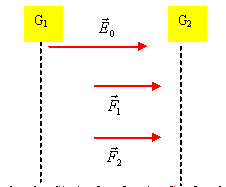Définir le travail de la force F entre O1 et O2 et le calculer en fonction de e, E et O1O2.     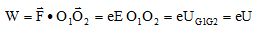Ce travail doit être moteur pour que les ions soient accélérés : or q=e, charge positive des ions, donc VG1-VG2 positive. Rappeler l'expression de l'énergie cinétique d'un ion en fonction de sa masse m et de sa vitesse v. Ec = ½mv2. En appliquant le théorème de l'énergie cinétique, déduire les expressions des vitesse v1 et v2 des ions lorsqu'ils arrivent en O2. Les vitesses initiales des ions étant négligeables : ½m1v12-0 = ½m2v22-0 =eU. v1 = (2eU/m1)½ ; v2 = (2eU/m2)½ . .. .. 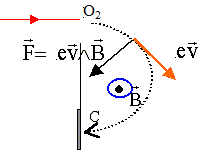Sens du champ magnétique B, régnant dans la chambre de déviation, pour que les ions puissent atteindre le collecteur : Dans la chambre de déviation, la force F est perpendiculaire au vecteur vitesse et au vecteur champ magnétique : la trajectoire des ions est plane et située dans un plan perpendiculaire à B et contenant le vecteur vitesse. La force électromagnétique est à chaque instant perpendiculaire au vecteur vitesse. 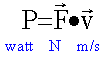Or en conséquence la puissance de la force électromagnétique est nulle. Cette force ne travaille pas et ne modifie pas l'énergie cinétique, et donc la valeur de la vitesse de la particule chargée. le mouvement de la particule chargée est donc uniforme dans la chambre de déviation. . Pour étudier ce mouvement on utilise le repère de Frenet.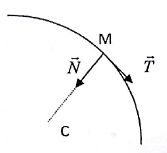 On appelle rayon de courbure au point M la longueur CM=r qui représente le rayon du cercle tangent à la courbe en M. 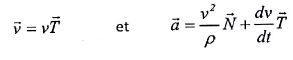Dans ce repère, les vecteurs vitesse et accélération sont donnés par les expressions : Donner les expressions des vitesses et accélérations des ions de masse m1 et m2 en fonction de v1, v2, r1 et r2. Le mouvement étant uniforme dv/dt = 0 ; 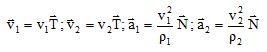Appliquer la seconde loi de Newton à chacun des ions et en déduire que la trajectoire est un cercle de rayon r1 ou r2. Donner les expressions de  r1 et r2 en fonction de m1, m2, e, U et B. Dans le repère de Frenet écrire la seconde loi de Newton sur l'axe N. La particule chargée n'est soumise qu'à la force de Lorentz, centripète. d'où eviB= mivi 2/ ri soit ri = mivi /(eB) or vi =[2 e U / mi]½ ; ri =[2 mi U / (eB2)]½ avec i = 1, 2. ri est constant : la trajectoire est un cercle. 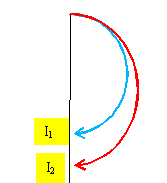Reproduire le schéma de la chambre de déviation et y représenter les trajectoire des deux ions. On observe sur la plaque photosensible deux taches I1 et I2 correspondant aux impact des ions de masse m1 et m2 respectivement. On observe sur la plaque photographique des taches Ti correspondants aux impact des ions provenant de l'ionisation de l'acide crotonique. L'impact le plus éloigné du point O2 est dû au cation le plus lourd appelé ion moléculaire. O2T = 0,676 m. En déduire la masse de cet ion ainsi que la masse molaire moléculaire de l'acide crotonique. U = 4,00 kV et B = 0,250 T. r2 =2 m U / (eB2) ; m = e(B r)2 / (2U) =1,60 10-19*(0,250*0,676/2)2 / 8000 =1,43 10-25 kg. M = m NA =1,43 10-25 *6,02 1023 = 8,60 10-2 kg /mol = 86,0 g/mol. Une analyse précise permet de détecter une tache moins intense, plus éloignée de O2 et distante de la précédente de 3,60 mm. A quelle masse molaire cette tache correspond-elle ? Interpréter. m = e(B r)2 / (2U) =1,60 10-19*(0,250*0,6796/2)2 / 8000 =1,443 10-25 kg. M = m NA =1,443 10-25 *6,02 1023 ~ 8,70 10-2 kg /mol = 87,0 g/mol. Cette tache est due à l'isotope 13C de l'élément carbone.

menu