Mathématiques. Concours ENSM 2014 filière professionnelle machine

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .


Question 1.
Une personne possède une certaine somme qu’elle désire partager inégalement entre trois bénéficiaires A, B, C respectivement et proportionnellement aux nombres 9, 8, 7. Après réflexion, elle change ses dispositions et fait le partage proportionnellement à 8, 7, 6.
Déterminer pour quel bénéficiaire le changement des dispositions est favorable, indifférent et défavorable.
On note a, b et c les parts de chacun : a + b + c = S ; a = 9 k ; b = 8 k ; c = 6 k avec k une constante.
(9+8+7) k = S ; k = S/24 ; a = 9S/24 =0,375 S ; b = 8S/24 ~0,333 S ;  c = 7S/24 ~0,292 S.
Partage après réflexion : on note a', b' et c' les nouvelles parts.
a' + b' + c' = S ; a' = 8 k' ; b' = 7 k' ; c' = 6 k' avec k' une constante.
(6+8+7) k' = S ; k' = S/21 ; a' = 8S/21~0,381 S ; b' = 7S/21~0,333 S ; c' = 6S/21~0,286S.
A est favorisé ; pour B, rien ne change ; C est défavorisé.
L’un des bénéficiaires a 200 euros de moins à la suite du changement des dispositions.
Calculer la valeur de la somme partagée et celle des trois parts.
(7/24-6/21)S = 200 ; (7*21-6*24) S = 200*21*24 ; 3S = 100 800 ; S = 33600 ; k' = 1600.
Part de A : 8*1600 = 12 800 ; part de B ; 7*1600 =11 200 ; part de C : 6*1600 = 9600.
Question 2.
Résoudre dans R les équations suivantes :
 4 x² - 2 x + 5 = 2 x + 4 ; 4x2-4x+1 =0 ; (2x-1)2=0 ; solution : x = ½.
.
.




Question 3.
Au jeu de la bataille navale, chaque joueur (A et B) a un carton quadrillé dont les cases sont notées de A à H et de 1 à 8 et sur lequel sont schématisés en gris quatre bateaux de tailles différentes et qui ne peuvent pas se toucher.
A tour de rôle, les joueurs annoncent une case. Le joueur adverse répond : « touché » si la case désignée est grise et « à l’eau » dans le cas contraire. Voici le carton du joueur A :

C’est le premier tour du joueur B. Déterminer la probabilité P(1) que le joueur A lui réponde « touché », puis la probabilité P(2) qu’il réponde « à l’eau ».
Nombre de cases : 64 ; nombre de cas favorables : 14 ; P(1) = 14/64 ; P(2) = (64-14)/64 = 50/64.
Au bout de vingt-deux tours, le joueur B a « touché » six fois et coulé deux bateaux mais « raté » les autres tours dont deux tours « à l’eau » à une case près des bateaux coulés.
 Calculer la probabilité P(3) qu’il touche un bateau du joueur A au tour suivant.
Le texte initial reste imprécis sur la sigification " coulé " et "une case près des bateaux coulés".
Il rest pour chaque joueur 64-11 = 53 tours. Il faut retrancher le nombre de cases situées près des bateaux coulés.
Nombre de cas favorables : 14-6 = 8.

.
Question 4.
Soit f la fonction définie sur l’intervalle ]0 ;+oo[ par f(x) = 1-3/(5x). On appelle (C) sa courbe représentative dans un plan muni d’un repère orthogonal (0, i , j )
Calculer la valeur de x pour que f(x) soit nulle.
0 = 1-3/(5x) ; 1 =3/(5x) ; 5x =3 ; x = 3/5.
Calculer la dérivée de f et donner son tableau de variation.
f ' = 3/(5x2).
 Calculer les coordonnées du point d’intersection noté I entre la courbe C et la droite d’équation : x = 1.
xI = 1 ; yI = 1-3/5 = 2/5.
Construire la courbe C en plaçant le point I.

Question 5.
Une suite arithmétique est définie par son premier terme de 1520 et sa raison de 65.
Calculer les termes de rang 4 et 127.
Terme de rang 4 : 1520+3*65 = 1715 ; terme derang 127 : 1520+65*126=9710.



Question 6.
On considère les deux nombres complexes suivants :
 zA a pour module 12 et pour argument 30° ; zB = - 7 - 9.i.
Ecrire les complexes zA, zA.zB et zA/zB  sous forme algébrique au centième près si besoin.
Ecrire le complexe zB sous forme trigonométrique au centième près si besoin.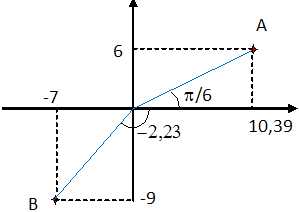

zA = 12(cos 30 + i sin 30) =12*0,866 +12*0,50 i = 10,3923+6 i.
zA =12 exp( ip/6) ; module de zB = (49+81)½ =11,4017 ; argument de zB : tan q =9/7 =1,2857; q =0,90975±p  =-2,2318 rad ; zB =11,4017 exp( -2,2318 i).
zB =11,4017 (cos (-2,2318) +i sin (-2,2318)).
Produit : faire le produit des modules et ajouter les arguments. zA . zB =12*11,4017 exp(-2,2318 +p/6)i )=136,821 exp(-1,7082 i) = 136,821( cos (-1,7082)+i sin(-1,7082)= -18,74 -135,53 i.
Autre méthode : (10,3923 + 6i) (-7-9i)=10,3923*(-7)+6*9-7*6 i -9*10,3923 i = -18,75 -135,53 i.

Quotient : faire le quotient des modules et soustraire les arguments : zA / zB =12/11,4017 exp( p/6+2,2318)i )=1,05247 exp(2,7616 i) = 1,05247(cos 2,7616 +i sin 2,7616) = -0,977 +0,390 i.
zA / zB = -0,98 +0,39 i.
Autre méthode : (10,3923 + 6i) /  (-7-9i)=(10,3923 + 6i) * (-7+9i) / (49+81)=(10,3923*(-7)-54-42 i +10,3923*9 i) / 130 = -126,7461 /130 +51,5307 i /130 = -0,97 +0,40 i.



  

menu