Equilibre,
projectile, dipôle RLC série, roue de Barlow.
Concours ENSM
2014 filière professionnelle machine.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Question
1.
Deux masses m1 = 5 kg et m2
disposées sur un double plan incliné parfaitement lisse sont reliées
entre elles par un fil inextensible de masse négligeable qui passe sans
frottement sur une poulie O. Les plans inclinés sur lesquels reposent m1
et m2 forment respectivement un angle a1
=p/6 rad
et a2
=p/3 rad avec l’horizontale. L’ensemble est à l’équilibre statique. On
considère que l’intensité de la pesanteur vaut 10 m.s-2.
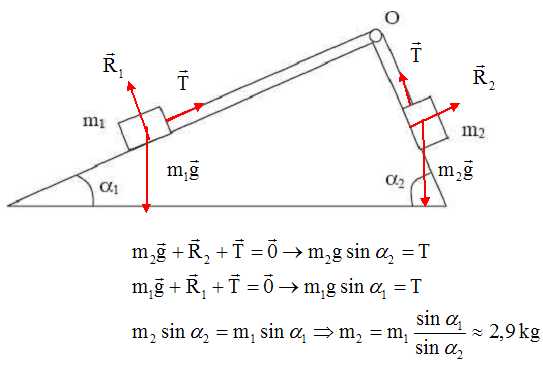
Reproduire
la figure en faisant apparaître les différentes forces qui s’appliquent
sur chaque masse. Définir ces différentes forces et donner leurs
caractéristiques. Calculer la valeur de m2.
Chaque solide est soumis à son poids, vertical, vers le bas,
valeur mg, à l'action du plan, perpendiculaire au plan et à la tension
du fil, parallèle au fil, dirigée ves la poulie.
|
| .
. |
|
|
Projectile.
Un projectile de masse 5 kg est lancé par un canon dont le tube a une
longueur L= 1,5 m. La durée du trajet dans le canon est de 0,04 s. On
considère que l’accélération de la pesanteur vaut 10 m.s-2.
En supposant constante la poussée des gaz de la poudre, le mouvement du
projectile dans le tube est uniformément accéléré :
Calculer
l’accélération de ce mouvement et la vitesse du projectile à sa sortie.
L = ½at2; la vitesse et la position étant nulles.
a = 2L/t2 = 3,0 / 0,042
=1,875 103 ~1,9 103 ms-2.
v0=
at = 1,875 103
*0,04 =75 m/s.
Calculer
la force propulsive des gaz résultant de la combustion de la poudre.
Le poids du projectile est négligeable devant la poussée ; poussée = m
a = 5*1,875 103
~9,375 103 ~9,4 103 N.
On
néglige la résistance de l’air. L’axe du tube faisant un angle a =p/4 rad avec
l’horizontale et l’extrémité ouverte du tube du canon étant l’origine
d’un repère orthonormé dont l’axe des abscisses est l’horizontale et
l’axe des ordonnée est la verticale.
Exprimer les
équations horaires de la trajectoire du projectile projetée sur l’axe
des abscisses et sur l’axe des ordonnées que l’on note respectivement :
x = f(t) et y = f(t) et l’équation de la trajectoire du projectile
liant y à x telle que : y = f(x).
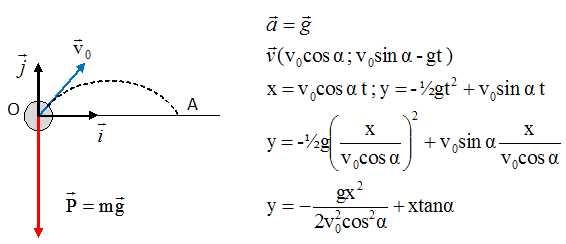
Calculer
l’abscisse du point d’impact A du projectile et la durée de sa
trajectoire.
yA=0
; -10xA2 / (2*752*cos245)+xAtan45
=0 ; -1,778 10-3xA+1=0
; xA=562
~5,6 102 m.
t = xA/(v0
cos a)
=562/(75 *cos45)= 10,6 ~11 s.
|
.
|
|
Dipôle
RLC série.
Un condensateur de 20 µF et une bobine d’inductance variable sont
connectés en série. La résistance de la bobine est de 100 ohms et son
inductance est réglée à 0,1 H. L’ensemble est relié
à un générateur dont la valeur efficace de la tension est U = 220 V à
la fréquence de 50 Hz.
Calculer
le
courant fourni par le générateur et son déphasage par rapport à la
tension.
Impédance Z =[ (r2 +(Lw-1/(Cw))2]½
avec w =
2 p f =
2*3,14*50 = 314 rad/s.
Z= [(1002 +(0,1*314-1/(20 10-6*314))2]½=162,3
ohms ; I = U /Z = 220/162,3 =1,3557 ~1,4 A.
tan j
= (Lw-1/(Cw)) / R =
(31,4-159,2) / 100 =-1,278 ; j
= -0,907 ~-0,91 rad.
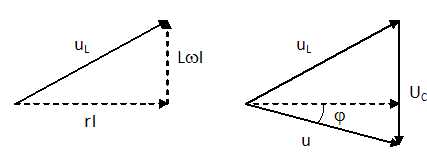
Calculer
les valeurs efficaces des tensions UL aux
bornes de la bobine et UC aux
bornes du condensateur.
UC =I/(Cw))
= 1,3557 /(20 10-6*314))=215,9
~216 V.
UL = (r2+(Lw)2)½I
=(1002+(0,1*314)2)½*1,3557
=142 V.
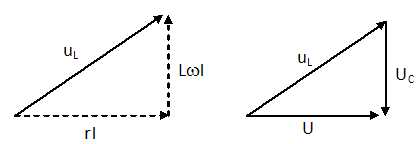
On modifie ensuite l’inductance de la bobine de façon à
rendre maximum le courant fourni par le générateur.
Calculer la
valeur de réglage de l’inductance.
Lw = 1/(Cw) ; L = 1/(Cw2)=1/(20 10-6*3142)=0,507
~0,51 H.
Calculer
le courant fourni par le générateur et son déphasage par rapport à la
tension.
Intensité et courant sont en phase ; I = U/r = 220/100 = 2,2 A.
Calculer
le nombre de condensateurs de capacité 5 µF à associer en série ou en
parallèle, pour que la capacité résultante soit de 20 µF.
Associer
4 condensateurs de 5 µF en parallèle.
|
|
|
Roue
de barlow.
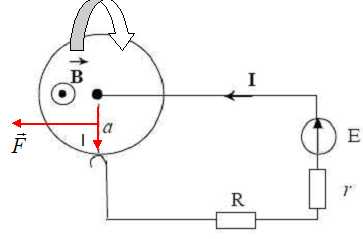
Une roue de Barlow, de rayon a = 0,30 m, est placée dans un champ
magnétique uniforme d’induction B = 0,6 T, perpendiculaire au plan de
la roue, dont le sens est indiqué sur la figure ci-dessous. La roue de
Barlow est placée en série avec un générateur de tension dont la force
électromotrice vaut E = 9 V et la résistance interne r = 4 ohms. La
liaison de la roue de Barlow avec le circuit est uniquement électrique
par contact glissant et la résistance du circuit électrique vaut R = 2
ohms.
Dans
le cas où l’on empêche la roue de tourner, déterminer les
caractéristiques de la force électromagnétique dite de Laplace. Montrer
sur un schéma le sens de rotation de la roue.
F =
I a B ; I = E/(r+R) = 9/(4+2) =1,5 A ; F = 1,5*0,30*0,6 =0,27 N.
Dans le cas où la roue tourne à la fréquence de rotation constante de
12 tours.s-1, calculer :
la
valeur de la force contre-électromotrice induite ;
e = B a v avec v =wa
= 12*6,28 *0,3 = 22,6 m/s ; e = 0,6*0,3*22,6 =4,07 ~4,1 V.
l’intensité
du courant parcourant le circuit ;
I=(E-e)/(R+r) = (9-4,07)/6 =0,8217~0,82 A.
la
valeur de la force électromagnétique dite de Laplace.
F= IaB = 0,82 *0,3*0,6 ~0,15 N.
|
|
|