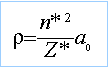Chimie
de l'étain : formes cristalline et complexation par les ions fluorure.
Concours inspecteur Dgccrf
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Les
deux formes cristallines de l'étain.
L'étain existe sous deux formes cristallines. L'étain blanc cristallise
dans une structure de masse volumique rblanc
= 7,27 g cm -3, et l'étain gris dans une
structure diamant, de masse volumique rgris
= 5,77 g cm-3 et de paramètre de maille noté a.
Le phénomène de "peste de l'étain" a été observé par les soldats de
Napoléon lors de la campagne de Russie. Leurs boutons d'uniforme, faits
d'étain, tombaient en poussière lors des grands froids à cause d'une
modification de structure cristalline entre ces deux formes, trop
rapide au delà de -40°C.
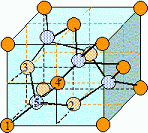
Représenter
la structure cristalline de l'étain gris.
La structure de type diamant est
une maille cubique à
face centrée avec occupation de la moitié des sites tétraèdriques ( 4
sur 8) de façon alternée, ce qui donne finalement 8 atomes par maille
élémentaire.
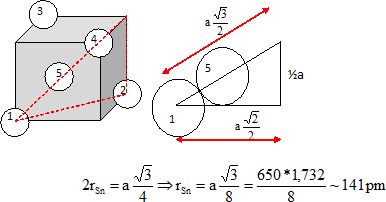
 Calculer
le rayon atomique de l'étain et comparer à la valeur tabulée de 145 pm.
Calculer
le rayon atomique de l'étain et comparer à la valeur tabulée de 145 pm.
Volume de la maille V = a3 m3.
Chaque maille compte en propre 8 atomes d'étain ; masse de la maille m
= 8 M(Sn)/NA =8*0,1178 / (6,02 1023)=1,57
10-24 kg.
rgris
= m/V =1,57 10-24
/ a3 ; a =(1,57 10-24
/5,77 103 )1/3 ~6,5 10-10 m.
 ( 1,2 %
d'écart avec la valeur tabulée ).
( 1,2 %
d'écart avec la valeur tabulée ).
A 25°C sous 1 bar, les entropies molaires standard de l'étain blanc et
de l'étain gris sont respectivement S°m (blanc) =26,36 J K -1mol -1
et S°m
(gris) =25,77 J K-1mol-1.
La transformation Sn blanc---> Sn gris
effectuée à 25°C et sous 1 bar, est associée à une variation
d'enthalpie DrH°(25°C)
=2220 J / mol.
Calculer
la variation d'enthalpie libre molaire au cours de cette même
transformation et conclure quant à la forme la plus stable de l'étain à
25°C.
DrS°(25°C) =S°m (gris) -S°m (blanc)
=25,77-26,36 = -0,59 J K-1mol-1.
DrG°(25°C)
=DrH°(25°C)
-T DrS°(25°C) =2220-298*(-0,59)=2396 J /mol.
Cette valeur étant positive, l'étain blanc est le plus stable à 25°C.
On cherche à estimer
le rayon atomique de l'étain, cette fois en utilisant le modèle de
Slater.
Indiquer
la structure lectronique de l'étain à l'état fondamental.
Z(Sn)=50.
1s2 2s2 2p6
3s2 3p6 3d10
4s2 4p6 4d10
5s2 5p2.
Définir
le rayon atomique d'un élément en utilisant une approche orbitalaire.
Le rayon atomique est égal à la moitié de la distance qui sépare les
deux noyaux d'atomes contigus dans un solide ou dans une molécule.
Calculer
le rayon atomique de l'étain dans le modèle de Slater et commenter
cette valeur.
Rayon de l'orbitale
de valence :
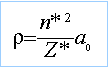
avec n*=4 et a0=52,9
pm ; s5p
=3*0,35+18*0,85 + 28*1 = 44,35.
Z*= Z-s5p =
50-44,35 =5,65.
Par suite r=
16/5,65*52,9 ~150 pm. ( 3,3 % d'écart avec la valeur des tables).
|
| .
. |
|
|
Etude
de l'étain en solution aqueuse.
Quels
sont les deux ions stables possibles dérivés de l'étain ? Justifier.
Les
formes stables correspondent à une couche électronique externe saturée.
Sn2+ : 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2.
Sn4+
: 1s2 2s2 2p6
3s2 3p6 3d10
4s2 4p6 4d10.
Etude électrochimique de
la complexation de l'ion étain (II) par les ions fluorure.
On étudie une pile constituée de deux demi-pile, reliées parun pont
salin :
Demi-pile 1 : solution aqueuse d'hexacyanocobaltate (II) de sodium et d'hexacyanocobaltate
(III) de sodium. Les concentrations des deux espèces sont de 1,0 10-3
mol/L, une électrode de platine plonge dans la solution.
Demi-pile 2 : solution aqueuse préparée par dissolution du chlorure
d'étain(II) à 1,0 10-3 mol/L, une électrode
d'étain plonge dans la solution.
Calculer
le pH de la solution de la demi-pile 2, et indiquer les concentrations
effectives en espèce Sn2+ et Sn(OH)+. pKa(
Sn2+/ Sn(OH)+) = 2,1 ; Ka
= 7,94 10-3.
|
avancement
volumique (mol/L) |
Sn2+
aq |
+ H2O |
= Sn(OH)+
aq |
+ H+aq |
| initial |
0 |
1,0 10-3 |
solvant |
0 |
0 |
| à
l'équilibre |
x |
1,0 10-3-x |
x |
x |
Ka
= [ H+aq][Sn(OH)+
aq] / [Sn2+
aq]=x2/(1,0 10-3-x).
(1,0 10-3-x)Ka
=x2
; x2
+7,94 10-3 x -7,94 10-6=0.
D
=(7,94 10-3)2+4*7,94 10-6=9,48
10-5 ; x = 8,97 10-4 ; pH
= - log( 8,97 10-4) =3,047 ~3,0.
|
.
|
|
Exprimer
en fonction des concentrations à l'équilibre les constantes globales de
formation des complexes Co(CN)64-
et Co(CN)63-
respectivement notées Kc1 et Kc2.
Co2+aq
+ 6 CN-aq = Co(CN)64-
aq ; Kc1
=[Co(CN)64-
aq]
/ ([Co2+aq][CN-aq]6).
Co3+aq + 6 CN-aq
= Co(CN)63-
aq ; Kc2
=[Co(CN)63-
aq]
/ ([Co3+aq][CN-aq]6).
Exprimer
en fonction des potentiels standard la grandeur DpKc = pKc1-pKc2. Faire
l'application numérique.
Kc1 / Kc2
=[Co(CN)64-
aq]
[Co3+aq]/ ([Co2+aq][Co(CN)63-
aq]
)
log(Kc1
/
Kc2 )=log([Co(CN)64-
aq]
/[Co(CN)63-
aq]
)+log ([Co3+aq]/[Co2+aq]).
DpKc
=-log(Kc1
/
Kc2 ) =log([Co(CN)63-
aq]
/[Co(CN)64-
aq]
)-log ([Co3+aq]/[Co2+aq]).
[Co(CN)63-
]aq
+ e- = [Co(CN)64-
]aq ; E°([Co(CN)63-
aq]/[Co(CN)64-
aq)= 0,06 log ([Co(CN)63-
aq]
/[Co(CN)64-
aq]
) = -0,80 V.
[Co3+aq]+e-
=[Co2+aq] ;
E°( [Co3+aq]/[Co2+aq] ) = 0,06 log( [Co3+aq]/[Co2+aq] )= 1,84 V.
DpKc
= ( E°([Co(CN)63-
aq]/[Co(CN)64-
aq) - E°( [Co3+aq]/[Co2+aq] ))/0,06 =(-0,80 - 1,84)/0,06
=-44.
Calculer
le potentiel d'équilibre de chaque électrode et en déduire la fem E de
la pile..
E1 = E°([Co(CN)63-
aq]/[Co(CN)64-
aq) +0,06 log log([Co(CN)63-
aq]
/[Co(CN)64-
aq]
) =-0,80 V.
E2 = E°(Sn2+aq / Sn(s)
+0,03 log ( [Sn2+aq] = -0,14 + 0,03 log (1,0 10-3)
= -0,23 V.
E = E2
-E1
=-0,23 -(-0,80) =0,57 V.
Ecrire
l'équation chimique ayant lieu lorsque cette pile débite et calculer sa
constante thermodynamique d'équilibre K°.
2[Co(CN)64-
]aq +Sn2+aq =2[Co(CN)63-
aq]+Sn(s) ; K° = [[Co(CN)63-
aq]]2/([Sn2+aq][[Co(CN)64-
]aq]2).
log K° = ([[Co(CN)63-
aq]]2/([Sn2+aq][[Co(CN)64-
]aq]2))/0,03 = (0,80-0,14)/0,03 =22 ; K° = 1022.
On réalise une
deuxième pile presque identique à la précédente. La seule différence
est l'introduction dans le compartiment 2 de l'acide fluorhydrique et
du fluorure de sodium chacun à 0,1 mol/L. La réaction de complexation
que l'on supposera totale se produit entre les ions Sn2+
et trois équivalents d'ion fluorure. Les électrodes conservent la même
polarité que précédemment, on mesure maintenant une fem E' = 0,36 V.
Quel
est le nouveau potentiel d'équilibre de la demi-pile 2 ?
E' = E'2-E1 ; E'2= E' + E1
=0,36+(-0,80) = -0,44 V.
Quelle
est dans le compartiment 2 la forme prédominante de l'étain(II) ?
Ecrire le couple mettant en jeu les formes prédominantes du couple
Sn(II) / Sn(0) et calculer son potentiel satndard redox apparent.
La réaction de complexation est totale et
l'ion fluorure est en large excès. [Sn2+aq]~0 ; [ SnF3-
aq]
= 1,0 10-3 mol/L ; [F-aq]~0,1 mol/L.
Sn2+aq
+3F-aq = SnF3-
aq avec KC3 = [SnF3-
aq]/([F-aq]3[Sn2+aq]).
SnF3-
aq + 2e- = Sn(s) + 3F-aq
; E'2 =E°(SnF3-
aq/Sn(s))
+0,03 log ([SnF3-
aq] /[F-aq]3).
E°(SnF3-
aq/Sn(s))
=E'2
-0,03
log ([SnF3-
aq] /[F-aq]3) = -0,44 -0,03
log(10-3 / 0,13) = -0,44
V.
En
déduire la constante globale de formation entre les ion Sn2+ et les
ions fluorure et vérifier que l'hypothèse d'une réaction totale est
vérifiée.
E2 = E°(Sn2+aq
/ Sn(s)) +0,03 log ( [Sn2+aq] = E°(Sn2+aq
/ Sn(s) +0,03 log ([SnF3-
aq]/([F-aq]3KC3) = E°(Sn2+aq
/ Sn(s) -0,03 log KC3 +0,03 log ([SnF3-
aq]/([F-aq]3).
On identifie : E°(SnF3-
aq/Sn(s))
=
E°(Sn2+aq / Sn(s)
-0,03 log KC3.
log KC3 =( E°(Sn2+aq
/ Sn(s) -E°(SnF3-
aq/Sn(s)))
/ 0,03 = (-0,14 -(-0,44))/0,03 = 10 ; KC3 =1010.
KC3 est
très grande, la réaction de formation de SnF3-
aq est totale.
|
|
|