Modulation- démodulation d'amplitude. Concours CPR 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Il est fréquent qu'un signal se présente sous une forme inadaptée à sa transmission ou à son traitement. La modulation est le procédé permettant de transporter les caractéristiques de ce signal dans des domaines de fréquences où la propagation et le traitement sont possibles. La démodulation est l'opération inverse. On s'intéresse aux signaux hertziens audio qui s'étalent sur la plage de fréquence fmin =300 Hz ; fmax = 4,50 kHz. La réception d'une onde électromagnétique nécessite une antenne dont la dimension caractéristique est une demi-longueur d'onde. Quelle devrait être la taille d'une antenne permettant la réception des signaux audio considérés ? l = c / f ; lmax=3,00 108 / 300 =1,0 106 m ou 1000 km ; lmini=3,00 108 / 4500 =6,67 104 m ou 66,7 km. Le signal audio à transporter est appelé signal modulant. Les méthodes de modulation sont élaborées à partir d'une onde sinusoïdale pure, appelée porteuse ou signal porteur. Le résultat de la combinaison de ces deux signaux s'appelle signal modulé. Le signal modulant, noté e(t), s'exprime par : e(t) = Am cos (2pfmt). Le signal porteur p(t) est donné par : p(t) = Ap cos (2pfpt). Le signal modulé en amplitude est de la forme : s(t) = Ap[1+mcos (2pfmt)]cos (2pfpt) où m >0, indice de modulation. 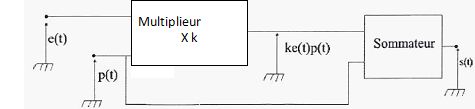Ce signal modulé a été obtenu en réalisant les opérations suivantes : Déterminer l'expression de l'indice de modulation m. Le signal modulé est obtenu en ajoutant au signal de la porteuse le produit k e(t) p(t). s(t) =p(t) + k e(t) p(t) =p(t) [1+ke(t)]=Ap cos (2pfpt) [1+kAm cos (2pfmt)]. On identifie m = kAm. On a enregistré au laboratoire un signal modulé. 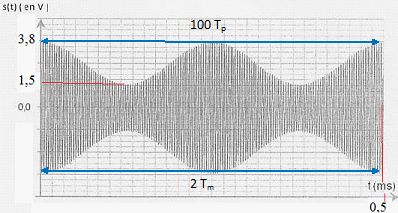Déterminer les valeurs de fp, fm et m. Tp = 0,0005 / 100 =5 10-6 s ; fp=1/Tp =1/(5 10-6) =200 kHz. Tm = 0,0005 / 2 =2,5 10-4 s ; fp=1/Tp =1/(2,5 10-4) =4 kHz. m =(3,8-1,5) / (3,8+1,5) ~0,4. . . Donner le spectre de s(t). Le spectre d'un signal désigne la représentation de l'amplitude des signaux sinusoïdaux qu'il contient en fonction de leurs fréquences respectives. s(t)= Ap cos (2pfpt) +kAm Ap cos (2pfpt) cos (2pfmt). cos (2pfpt) cos (2pfmt) = ½cos(2p(fp+fm)t) +½cos(2p(fp-fm)t). s(t)= Ap cos (2pfpt) + ½kAm Ap cos(2p(fp+fm)t) +½kAm Apcos(2p(fp-fm)t). (fp ; Ap), (fp+fm ; ½kAm Ap ), (fp-fm ; ½kAm Ap ). On envoie dans la pratique un signal modulant audio, somme de signaux sinusoïdaux qui encombrent la plage de fréquence 300 Hz - 4,5 kHz. La fréquence de la porteuse est 185 kHz. Quelle est la bande passante d'un filtre nécessaire à la transmission intégrale du signal s(t) au niveau de l'antenne ? fp+fm-(fp-fm) = 2fm = 2*4,5 = 9 kHz. . La figure ci-dessous représente le principe de fonctionnement du circuit de démodulation situé après l'antenne réceptrice. 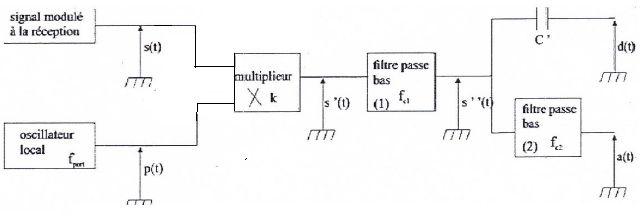Donner le spectre du signal s'(t) obtenu à la sortie du multiplieur. s'(t) = Ap cos (2pfpt) [1+ k s(t)]. s(t)= Ap cos (2pfpt) + ½kAm Ap cos(2p(fp+fm)t) +½kAm Apcos(2p(fp-fm)t). s'(t) = Ap cos (2pfpt) [1+ k Ap cos (2pfpt) + ½k2Am Ap cos(2p(fp+fm)t) +½k2Am Apcos(2p(fp-fm)t)]. s'(t) = Ap cos (2pfpt) + ½k A2p (1+cos (4pfpt))+0,25k2Am A2pcos(2p(2fp+fm)t) +0,25k2Am A2pcos(2pfm)t) +0,25k2Am A2pcos(2p(2fp-fm)t)+0,25k2Am A2pcos(2p(fm)t). s'(t) =½k2 A2p +Ap cos (2pfpt) +½k A2p cos (4pfpt) +0,25k2Am A2pcos(2p(2fp+fm)t) +0,5k2Am A2pcos(2pfm)t) +0,25k2Am A2pcos(2p(2fp-fm)t). (0 ; ½k2 A2p), (fp ; Ap),  (2 fp; ½k A2p ), (2fp+fm ; 0,25k2Am A2p ), (fm ; 0,5k2Am A2p ), ( 2fp-fm ; 0,25k2Am A2p). (0 ; ½k2 A2p), (fp ; Ap),  (2 fp; ½k A2p ), (2fp+fm ; 0,25k m A2p ), (fm ; 0,5 k m A2p ), ( 2fp-fm ; 0,25k m A2p). Le filtre passe bas 1 a une fréquence de coupure fc1 telle que fm<fc1<fp et Le filtre passe bas 2 a une fréquence de coupure fc2 telle que fc2<fm. On considèrera dans un premier temps que les filtres sont parfaits. C'est à dire que chaque filtre admet un gain unité pour les fréquences inférieures à sa fréquence de coupure et un gain nul pour toute fréquence supérieure à sa fréquence de coupure. Donner le spectre du signal s"(t). Le filtre 1 élimine toutes les fréquences supérieures à fp. (0 ; ½k2 A2p),  (fm ; 0,5 k m A2p ). Déterminer le spectre du signal d(t). Le filtre 2 élimine la composante (fm ; 0,5 k m A2p ) ; il reste a(t)= (0 ; ½k2 A2p). le condensateur C' élimie la composante continue (0 ; ½k2 A2p) ; d(t) = (fm ; 0,5 k m A2p ) ou (fm ; 0,5 k2 Am A2p ) Montrer que l'on peut reconstituer le signal e(t). e(t) = d(t) / (0,5 k2  A2p) = d(t) / a(t).

menu