Mathématiques : concours agent spécialiste de la police technique et scientifique Rennes 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Le nombre 158 est un multiple de 2, 3, 5, 7. 158 est pair.   Que vaut 5-6 /2+ 4 ? 3,5 ; 6 ; -2 ; 4. 6/2 =3 ; 5-3+4 = 6. Quel est l'inverse de 2 /5 ? -2 / 5 ; 5 / 2 ; 2,5 ; -2,5. En utilisant 42 roses et 36 tulipes, quel est le nombre maximal de bouquets identiques que l'on peut former ? 2 ; 3 ; 6 ; 12. 42 =2*3*7 ; 36 = 22*32 ; PGCD(36 ; 42 ) =6. Que vaut : 3/ 5 +3/5 *2 / 3 ? 6 /5 ; 9 / 20 ; 12 /30 ; 1. 3 /5 ( 1+2 /3) =3 /5 (3 /3 +2 /3) =3/5 (5 /3) =3*5 /(5*3) =1. (a4 x a-2)-1 /a3 est égal à : a4 ; a-5 ; a5 ; a-24. (a4-2)-1 /a3 =(a2)-1 /a3 =a-2 /a3 =a-2-3 =a-5. L'écriture scientifique de 65 100 000 est : 6,51 107 ; 651 105 ; 6,51 10-7 ; 651 10-5. Quel est le PGCD de 240 et 375 ? 5 ; 15 ; 25 ; 35. 240 = 24*10 = 23*3*2*5 =24*3*5 ; 375 = 25*15 =3*53. PGCD(240 ; 375 = 3*5 = 15. (3x-2)2 est égal à : 9x2-4 ; 3x2-12x-4 ; 9x2-12x+4 ; 9x2+12x-4. Un véhicule effectue 50 km en 2 h puis 100 km en 3 h. Quelle est sa vitesse moyenne 'n km/h) ? 25 ; 30 ; 33 ; 68 (50 +100 ) / (2+3) =150 / 5 = 30. 6-4(x-2) est égal à : 2x-4 ; 14-4x ; -2-4x ;6-2x. 6-4x-4*(-2) =6-4x+8 =14-4x. Quelle est l'expression factorisée de 4x2-12x+9 ? (2x+3)(2x-3) ; (2x+3)2 ; (2x-3)2 ; on ne peut pas factoriser cette expression. Pour x =-2, l'expression 5x2+2x-3 est égale à : 13 ; -27 ; -17 ; 17. 5(-2)2+2(-2)-3=5*4 -4 -3 = 20-7 =13. Le nombre 1 est solution de l'inéquation  : -2x +1 <= -3 ; 5x+3 <9 ; 2x+4 <=8 ; 4x-3 >7. -2(1) +1 =-2+1 =-1 ; -1 est supérieur à -3 ; 5*1+3 =8; 8 est inférieur à 9 ; 2*1+4 =6 ; 6 n'est pas inférieur ou égal à 8. 4*1-3 =1 ; 1 n'est pa supérieur à 7. . . 4 10-3 / (5 102) est égal à : 0,000 000 8 ; 8 10-6 ; 0,8 10-6 ; 8 10-7. 4 /5 10-3-2 =0,8 10-5 =8 10-6. Racine carrée (500) -racine carrée (45) est égal à :  7 racine carrée (5) ; racine carrée (455) ; 15,65 ; 91 racine carrée (5). 500 =5 *100 =5*102 ; racine carrée (500) = 10 racine carrée (5) ; 45 =9*5 =32*5 ; racine carrée (45) = 3 racine carrée (5). Les solutions de (3x-2)(x+5)=0 sont : 2/3 et -5 ; 3/2 et -5 ; -2/3 et 5 ; -3/2 et 5. 3x-2 = 0 ; x = 2/3 et x+5=0 ; x=-5. En 3è A, sur 30 élèves il y a 40 % de filles. En 3è B, sur 20 élèves, il y a 60 % de filles. Lorsque les deux classes sont réunies, quel est le pourcentage de filles ? 24 % ; 36 % ; 48 % ; 50 %. 30*0,4 = 12 filles en 3è A et 20*0,60 =12 filles en 3è B. 24 / 50 = 48 %. La moyenne de cette série de valeurs : 7 ; 8 ; 8 ; 12 ; 12 ; 14 ; 15 ; 15 ; 44 est égale à :9 ; 12 ; 13,5 ; 15. (7+8+8+12+12+14+15+15+44) / 9=15. Diminuer un prix de 15 % revient à : multiplier ce prix par 1,15 ; diviser ce prix par 0,85 ; diviser ce prix par 1,15 ; multiplier ce prix par 0,85. . Un artcicle coûtant 120 € baisse de 5 %. Quel est son nouveau prix ? 6 € ; 119,5 € ; 114 € ; 126 €. 120*0,95 =114 €. Une voiture roule à vitesse constante de 90 km/h. En combien de temps parcourt-elle 150 km ? 2 h ; 1 h 36 min ; 140 min ; 100 min. 150/90 =1,66 h ou 1 h 40 min ou 100 min. Un jeu de construction est composé de 5 cubes bleus, 3 cubes rouges, 7 cubes verts, 2 cubes jaunes et 8 cubes blancs. Tous les cubes sont identiques et rangés dans un sac opaque. On tire au hasard un cube. Quelle est la probabilité de tirer un cube dont la couleur est l'une des couleurs du drapeau français ? 0,25 ; 0,4 ; 0,64 ; 0,75. Nombre de cas favorables : 5 + 3 +8 =16 sur 25 cas possibles ; 16/25 = 0,64.  Dans un triangle rectangle, pour calculer la longueur de l'hypothènuse, on utilise  : le théorème de Thalès ; la réciproque du théorème de Phytagore ; le théorème de Phytagore ; la réciproque du théorème de Thalès. Dans un triangle rectangle, on veut calculer la valeur d'un angle aigu. On connaît la longueur du côté opposé et du côté adjacent de cet angle. On utilise alors : le cosinus ; le sinus ; la tangente ; le théorème de Phytagore. IJK est un triangle rectangle en I. IK = 2,7 cm ; KJ = 4,5 cm. La longueur du côté IJ est (en cm) :12,96 ; 3,6 ; 1,8 ; 5,2. IJ2 = KJ2-IK2 =4,52-2,72 =12,96 ; IJ = 3,6 cm. Le volume exact d'une boule de 3 cm de rayon est  ( en cm3) :12 p ; 37,68 ; 36 p ; 113,04. 4/3 p R3 =4/3p33=36 p. La section d'un cylindre de révolutionpar un plan parallèle à son axe est : un cercle, un rectangle, un trapèze, une éllipse. La section d'une pyramide, dont la base est un carré, par un plan parallèle à sa base est : un parallèlogramme non rectangle, un triangle isocèle, un rectangle non carré, un carré. Un rectangle A'B'C'D' d'aire 24 cm2 est l'agrandissement à l'échelle 1,25 d'un rectangle ABCD. Quelle est l'aire du rectangle ABCD ( en cm2) ? 15,36 ; 19,2 ; 30 ; 37,5. 24 / 1,252 =15,36 cm2. Le théorème de Thalès sert : à calculer une longueur, à démontrer qu'un triangle est rectangle ; à démontrer que deux droites sont parallèles ; à calculer la mesure d'un angle. Henry a reçu pour son anniversaire un bocal cylindrique de diamètre 30 cm. Il le rempli partiellement d'eau et y plonge un poisson. La hauteur de l'eau dans le bocal augmente de 3 mm. Avec ces données : on ne peut rien calculer ; on peut calculer le volume du poisson ; on peut calculer le volume du bocal ; on peut calculer le volume d'eau initial. Volume du poisson : 0,3 *3,14*152 =212 cm3. Dans un triangle ABC rectangle en A, on donne AB = 6 cm et BC =12 cm. La valeur de l'angle ACB arrondie au degré près est : 30° ; 53° ; 60° ; 90°. sin ACB =6/12 = 0,5. L'angle ACB mesure 30 °. 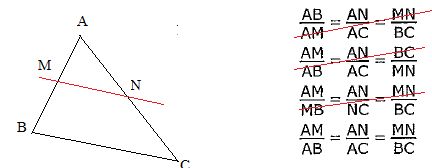Dans le triangle ABC, on a M appartenant à [AB], N appartenant à [AC] et MN parallèle à [BC]. 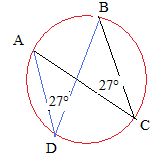Dapère le théorème de Thalès : Soit un cercle de centre O, et A, B, C et D quatre points distincts du cercle. On donne l'angle ACB =27°. Alors l'angle ADB mesure : 90° ; 53° ; 27° ; on ne peut pas savoir. 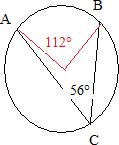Soit un cercle de centre O et A, B, C trois points distincts de ce cercle. On donne l'angle ACB = 56°. Alors l'angle AOB mesure :180° ; 124° ; 112° ; on ne peu pas savoir. A et B sont symétriques par rapport à la droite (d) Alors (d) est : la bissectrice du segment [AB], la médiatrice du segment [AB], la médiane du segment [AB], la hauteur du segment [AB].. La forme générale d'une fonction affine est :  f(x) = ax ; f(x) = ax2 ; f(x) = ax2+b ; f(x) = ax+b. une tension efficace ; une tension maximale ; une période. La représentation d'une fonction affine est  : une droite, une hyperbole, une parabole, une éllipse. L'image de 2 par la fonction affine f(x) = -3x+4 est :-1 ; -2 ; 1 ; 2. f(2) =-3*2+4 = -6+4 = -2.

menu