Mathématiques : concours agent spécialiste de la police technique et scientifique Lyon 2013

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .


.
.


Souligner la seule affirmation vraie.
L'expression (2x+1)2-(3x-2)2 est égale à :
(5x-1)(x-1) ; (5x+3)(-x-1) ; (5x-1)(-x+3) ; (2x+1)(3x-2).
(2x+1+3x-2)(2x+1-(3x-2))=(5x-1)(-x+3).
 Quelle est la bonne égalité ?
(-5x-6)2=-(5x-6)2 ; (-5x-6)2=(5x+6)2 ; (-5x-6)2=-(5x+6)2 ; (-5x-6)2=25x +36.
Quelle est la forme développée et réduite de (3x-2)2 ?
9x2+4 ; 9x2-4 ; 9x2-12x +4 ; 9x2-6x-4.
Combien vaut racine carrée [(-3)2] ?
-3 ; - racinne carrée (32) ; 3 ; impossible pas de racine carrée négative.
Racine carrée (25) / racine carrée (9) est :
décimal, irrationnel, rationnel, irréductible. ( 5 / 3 ).
Laquelle des propositions suivantes est exacte ?

9*8 /8 +9 /8 = (72+9) / 8 = 81 / 8.
 5-(a+3) /3 est égal à :
(18-a)/3 ; 5-a ; (12-a) /3 ; (2-a) / 3.

Quelle est l'autre écriture de  
Les nombres 106 et 51 :
ont 0 comme PGCD ; ont 3 comme PGCD ; sont premiers entre eux ; ont -1 comme PGCD.
106 = 2*53 ; 51 = 3*17.
La solution de l'équation 1-x =1+x est le nombre 0 ; 2 ; -0,5 ; tous les réels positifs.
-x=+x ; 2x =0 ; x =0.
Un triangle équilatéral a pour mesure de côté x. Un rectangle a pour longueur x+2 et pour largeur x-5.
Pour quelles valeurs de x le périmètre du rectangle est-il inférieur ou égal à celui du triangle ?
0< x <=6 ; x<= 6 ; 5 < x <=6 ; imposible, aucune solution.
périmètre du triangle : 3x ; périmètre du rectangle : 2(x+2+x-5) = 4x-6.
4x-6 <=3x ; x-6 <=0 ; x<=6 ; de plus x doit être positif.
.
.



L'inéquation -5x <=0 a pour solution :
Tous les nombres négatifs ; tous les nombres positifs ; tous les nombres supérieurs ou égaux à -5 ; tous les nombres supérieurs ou égaux à 5.  -x <=0 ; x >=0.
Résoudre le système suivant par substitution : 3x+y=9 et 5x-2y=26.
y =9-3x ; 5x-2(9-3x) =26 ; 5x-18+6x=26 ; 11x =26+18 ;11x =44 ; x =4 ; y =9-3*4= -3.
Pour emballer quatre paquets et deux colis, il faut 42 m de ficelle. Pour un paquet et un colis, il en faut 15.
Quelle longueur de ficelle faut-il pour chaque article ?
On note x la longueur de ficelle pour emballer un paquet et y la longueur de ficelle por emballer un colis.
x+y =15 et 4x+2y=42 ; x =15-y ; 4(15-y)+2y=42 ; 60-4y+2y =42 ; 60-42 =2y ; y =9 et x =6.

Si on transfert trois billes du sac A vers le sac B, les deux sacs ont le même nombre de billes. Si on fait le contraire, le sac A contient deux fois plus de billes que le sac B.
Etablir un système de deux équations à deux inconnues .
A contient initialement x billes et B en contient y.
D'une part : x-3 =y+3 ; x-y =6.
D'autre part : x+3 =2(y-3) ; x+3 =2y-6 ; x-2y= -9.
Un objet subit une hausse de prix de 5 % puis une baisse de 5 %. Comment le prix a-t-il finalement varié ?
il a augmenté ; il a diminué ; il est resté le même ; les pourcentages s'annulent.
Pour un prix initiaal de 1 € : 1,05*0,95 =0,9975 €.

.
Un billet d'avion dont le prix initial était de 2000 € est désormais vendu 2500 €. Son prix a augmenté de : 500 % ; 20 % ; 25 % ; 10 %.
(2500-2000) / 2000 *100 =25 %.
La masse volumique d'un corps vaut 2 kg dm-3. 1 m3 de ce corps pèse : 2000 m3 ; 2 tonnes ; 20 kg ; 200 kg.
 Dans 1 m3 il y a 1000 dm3 ; 2*1000 = 2000 kg = 2 tonnes.
Le tableau de proportionnalité suivant correspond à une fonction linéaire. Qiel est le coefficient directeur ?
x8-16
f(x)-612
-6 / 8 =12 /(-16) = -0,75.
Voici une série de notes : 6 ; 9 ; 12 ; 14 ; 9. Quelle est l'étendue de la série ? 1 ; 12 ; 8 ; 14.
Ecart entre la plus petite et la plus grande : 14-6 = 8.
Le premier quartile d'une série statistique est forcément :
supérieur à la médiane ; inférieur à la médiane ; égal à la médiane ; inférieur ou égal à la médiane.
Dans une classe de 3è le temps hebdomadaire consacré au sport est donné dans le tableau suivant :
temps (h)t <1t < 2t < 3t < 4t < 6t < 8
Nombre d'élèves11014161920
 Le nombre d'élèves pratiquant entre 2 h et 3 h de sport est : 10 ; 14 ; 4  24.
Dans un magasin de tissu, les clients achètent différentes longueurs de tissu : voici les effectifs cumulés croissants des clients en fonction des longueurs achetées.
Longueur (m)123561020100
Effectif cumulé croissant1362020354551
Au moins un quart des longueurs achetées est inférieur à ( en mètres) : 3 ; 6 ; 10 ; 2.
Le quart de 51  est égal à environ 13 ; au moins un quart des longueurs achetées est inférieure à 6 m.




Une urne est composée de la manière suivante : 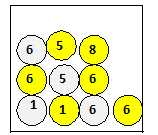On tire une boule au hasard.
Quelle est la probabilité de tirer une boule grise ? 4 /10 = 0,4.
On tire une boule  au hasard. Alors...
Il y a plus de chances de tirer  un numéro pair qu'un numéro impair.
Il y a autant de chances de tirer  un numéro pair qu'un numéro impair.
Il y a moins de chances de tirer  un numéro pair qu'un numéro impair.
Il y a plus de chances de tirer un numéro impair gris.
Un cible est formée de deux cercles concentriques de rayons respectifs 40 et 30 cm. On jette une fléchette sur la cible et elle l'atteint.
La probabilité qu'elle atteigne la zone noire est égale à : 1/4 ; 7/16 ; 1/5 ; 4/3.
Aire du grand disque : 3,14 *402  ; aire du petit disque : 3,14*302 ;  aire de l'anneau noir : 3,14(402-302) = 3,14*(40+30)(40-30) =3,14 *70*10.
Probabilité d'atteindre la zone noire : 3,14 *70*10 / (3,14*40*40) =7/ / (4*4) =7/16.
Par quel nombre doit-on multiplier les dimensions d'un objet si on désire que son aire soit multipliée par 16 , 16 ; 32 ; 4 ; 8.
L'aire d'une sphère de rayon 5 cm est ( en cm2) :31,4 ; 1884 ; 314 ; 628.
4 p R2 = 4*3,14*52=314 cm2.
 


  

menu