Mathématiques
:
concours agent spécialiste de la police technique et
scientifique Bordeaux 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Parmi les affirmations suivantes, indiquer celle(s) qui est ( sont) vraie(s) ?
1/8 est un nombre décimal. Vrai. ( 1/8 = 0,125).
72 a exactement 5 diviseurs. Faux. ( 1 ; 2 ; 3 ; 4 ; 8 ; 9 ; 12 ....)
Si n est un nombre entier, (n+1)(n-1) est toujours égal au carré d'un entier. Faux. ( (n+1)(n-1) = n2-1).
Deux nombres impairs sont toujours premiers entre eux. Faux ( 3 et 9 sont impairs mais ne sont pas premiers entre eux ).
L'expression numérique A est égale à : 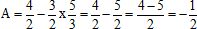
Dans
une entreprise qui fabrique des ampoules électrique, on contrôle la
production en testant la durée de vie d'un échantillon d'ampoules. On
obtient les résultats suivants.
Durée de vie ( h)
|
100
|
110
|
121
|
Nombre d'ampoules
|
4
|
6
|
5
|
|
|
|
|
Calculer la durée de vie moyenne.
(4*100 +6*110+5*121) / (4+6+5) =111 heures.
L'expression 15x+20-6x-11 est égale à :
9(x+1). Vrai. 15x-6x+20-11 = 9x+9 = 9(x+1).
9x2+9. Faux ; 18 x. Faux ;
est égale à 7 pour x = -2/9. Vrai. 9*(-2/9) + 9 = -2+9 = 7.
L'expression (2x-3)2-(x+2)2 est égale à :
(x-1)(3x-1). Faux. Différence de deux carrés : (2x-3+x+2)(2x-3-x-2)=(3x-1)(x-5).
(x-5)(3x-1). Vrai.
3x2-13. Faux.
3x2-16x+5. Vrai.
Le nombre B peut s'écrire : 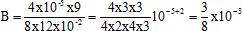
Entre Toulouse et
Bordeaux, il y a 210 km ; entre Toulouse et Lyon 360 km et ces trois
villes sont les sommets d'un triangle rectangle. Calculer la distance
Bordeaux Lyon à 1 km près.
Th de Phytagore : 3602 + 2102 = x2 ; x2 = 173700 ; x = 417 km.
|
| .
. |
|
|
Pour gérer son stock, un tailleur relève la taille de ses clients et dresse le tableau :
Taille ( cm)
|
130
|
145
|
155
|
160
|
170
|
175
|
180
|
190
|
Nombre de clients
|
3
|
5
|
11
|
25
|
36
|
20
|
8
|
2
|
La médiane vaut 165 cm. Faux.
La moitié des valeurs sont inférieures à la médiane, l'autre moitié est supérieure à la médiane ; il y a 110 clients, la taille 170 cm sépare les clients en deux partie égale.
La médiane vaut 170 cm. Vrai.
La moitié des clients mesure au plus 165 cm. Faux.
La moitié des clients mesure au moins 170 cm. Vrai.
Les équations (4x-6)(3x+2)=0 et (2/3x-1)(10x+15)=0 ont pour solution commune :
4x-6 =0 ; x = 6/4 = 3/2 et 3x+2=0 soit x = -2/3 ;
2/3x-1 = 0 soit x = 3/2 et 10x+15=0 soit x = -15/10 = -3/2.
Un cube a une arête de 11 cm et une masse de 968 g. La masse volumique du matériau qui le compose est : volume : 11*11*11 = 1331 cm3. Masse / volume = 968 / 1331 ~ 0,727 g cm-3 ou 727 kg m-3.
Calculer le débit en m3 heure-1 d'une pompe qui fournit 6 m3 en 2 h 24 min.
2 h 24 min = 2*60+24 = 144 min ou 144/60 =2,4 h ; débit : 6 / 2,4 =2,5 m3 h-1.
Une statue est formée d'un cône de rayon de base 1 m et de hauteur 2,5 m posée sur un cube d'arête 3,5 m.
Quel est le volume de cette statue à 1 m3 près ?
Volume du cube : 3,53 =42,875 m3 ; volume du cône : 3,14 R2H/3 = 3,14*2,5/3 = 2,616 m3 ; total : ~45 m3.
|
.
|
|
La fraction 345 / 645 est égale à : 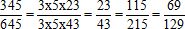
Un
ouvrier doit découper dans une plaque de longueur 110 cm et de largeur
88 cm des carrés identiques dont la longueur du côté soit un nombre
entier de cm. Quelles sont les longueurs possibles ?
110 = 2*5*11 ; 88 = 2*2*2*11 ; le côté du carré peut être 1, 2, 11 ou 22 cm ( diviseurs communs à 88 et 110).
A quoi est égal le nombre 3 fois racine carré de 2 ? 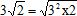
Un
loyer a augmenté de 2,5 % entre 2011 et 2012 puis de 4 % entre 2012 et
2013. De quel pourcentage le loyer a-t-il augmenté entre 2011 et 2013 ?
1,04 * 1,025 = 1,066 soit 6,6 % de hausse.
Une
promenade en mer est proposée à deux groupes. Le premier composé de 8
adultes et 3 enfants paie en tout 57 €, le second composé de 7 adulltes
et 5 enfants paie 57 €. Calculer le prix payé par un adulte et celui
payé par un enfant.
Soit x le prix payé par un adulte et y celui payé par un enfant :
8x+3y = 57 et 7 x +5y = 57.
ou 40 x +15y =285 et 21x + 15 y = 171 ; soustraire : 19x = 114 ; x =6 ; par suite y = 3.
Après une augmentation de 8 % un paquet de gâteau coûte 2,70 €. Calculer son prix avant augmentation.
2,70 * 100 / 108 = 2,5 €.
On donne l'égalité x(x-3)=x2-x-6 Cette égalité est vraie pour : x=-2. Faux. -2(-2-3) =+10 et (-2)2+2-6 =0.
x = 0. Faux. x = -3. Faux. -3(-3-3) =+18 et (-3)2+3-6 =6.
x = 3. Vrai. 3(3-3) = 0 et 32-3-6 = 0.
Résoudre le système suivant : x+2y =-4 et 3x+5y =-14,5.
3x+6y = -12 et 3x+5y =-14,5. Soustraire : y=2,5 ; par suite x = -9.
|
|
|