Marquage isotopique et imagerie médicale : sujet ASPF ( acueil, savoir, partage, francophonie) 2009

Marquage isotopique et imagerie médicale : sujet ASPF ( acueil, savoir, partage, francophonie) 2009

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Le marquage isotopique consiste à remplacer dans la molécule que l’on désire étudier, un atome ou un groupe d’atomes par un atome radioactif de manière à pouvoir l’utiliser comme traceur.
En cancérologie, le traceur utilisé pour l’imagerie médicale est le glucose marqué par le fluor 18. Ce traceur s’accumule préférentiellement dans les cellules cancéreuses, grandes consommatrices de sucre. Cette technique se singularise par l’utilisation d’isotopes radioactifs dont le temps de demi-vie est beaucoup plus court que les produits classiques de la médecine nucléaire. Ainsi le fluor 18 a un temps de demi-vie radioactive de 110 minutes.
Pour cette raison le traceur est fabriqué sur place de manière à ce qu’au moment de son injection au patient, la
dose administrée ait une activité de 260 MBq.
Désintégration du fluor 18.
Le fluor 18 ¹⁸₉F est un isotope radioactif du fluor. Il se désintègre pour donner de l'oxygène 18 ¹⁸₈O.
¹⁸₉F ---> ¹⁸₈O +^A_ZX.
Donner la composition du noyau de fluor 18.
9 protons et 18-9 = 9 neutrons.
Déterminer A et Z. Quel est le type de désintégration ? Justifier.
Conservation de la charge : 9 = 8 +Z d'où Z = 1.
Conservation du nombre de nucléons : 18 = 18 +A d'où A = 0.
¹⁸₉F ---> ¹⁸₈O +⁰₁e.
Emission d'un positon ⁰₁e, donc radioactivité de type ß⁺.
Constante radioactive du « fluor 18 »
Le laboratoire d’imagerie médicale est équipé d’un appareil qui permet de remplacer un groupement hydroxyle –
OH du glucose par un atome de « fluor 18 ». Le nombre N de noyaux radioactifs de « fluor 18 » encore présents
varie en fonction du temps et suit une loi de décroissance exponentielle : N = N₀.e^-lt.
La relation liant la constante radioactive et le temps de demi-vie est : t_½ = ln2 / l.
Donner la définition du temps de demi-vie.
Durée au bout de laquelle l'activité initiale est divisée par deux.
Quelle est l’unité de l dans le système international ? Calculer la valeur de l.
l = ln2 / t_½ =0,69 / (110*60) = 1,05 10^-4 s^-1.

.
.

L’équipe du laboratoire d’imagerie médicale doit réaliser 2 examens dans la matinée sur deux patients différents.
Deux doses différentes de traceur, D₁ et D₂, sont fabriquées en même temps avant leur injection pour réaliser ces
examens. Au moment de son injection au patient, la dose de traceur doit avoir une activité de 260 MBq. Lors du
premier examen on injectera la dose notée D₁à 9 h 00. On rappelle que l’activité A du « fluor 18 » présent dans le
traceur est reliée à la variation DN du nombre de noyaux radioactifs de cet isotope pendant une durée Dt par la
relation :
A = – DN / Dt
( si Dt est suffisamment petit, on peut écrire A = – dN/dt)
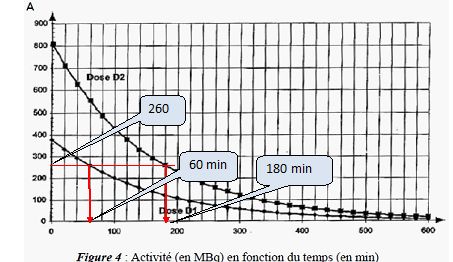
La mesure expérimentale de l’activité de chaque dose, toutes les vingt minutes, à partir de la date t = 0 min
(instant de fabrication), a permis de tracer le graphe A = f(t) représentés sur la figure ci-dessous.
On rappelle que : 1MBq = 10⁶ Bq.

Après avoir rappelé l’expression du nombre de noyaux radioactifs noté N encore présents à l’instant de date t, montrer que l’activité A de la source radioactive peut se mettre sous la forme : A = A₀.e^-lt. Exprimer littéralement A₀ en fonction de l et N₀.
N = N₀ e^-lt ; A =-dN/dt = l N₀ e^-lt ; on pose A₀ = l N₀ .

.

Calculer le nombre de noyaux de « fluor 18 » présents dans la dose de traceur au moment de son injection au patient lors de l’examen médical. On prendra pour l la valeur l » 1.10^-4 s^-1.
N₀ =A₀ / l =260 10⁶ / 10^-4 =2,6 10¹².
En s’aidant de la figure 4, déterminer l’heure de la fabrication de la dose de traceur notée D₁.
9 h -1h = 8 h.
A quelle heure le deuxième examen correspondant à l’injection de la dose notée D₂, préparée en même temps que la dose D₁, aura-t-il lieu ?
8 h + 3h = 11 h.
L’injection d’une dose D₃ a lieu à l’instant de date t_i.
Calculer l’ordre de grandeur, exprimé en heures, du temps nécessaire après l’injection pour que l’activité soit 100 fois plus faible qu’au moment de l’injection.
A = A₀ e^-lt ; 2,6 =260 e^-lt ; 0,01 = e^-lt ; ln 0,01 = -l t ; t = 4,6 / 10^-4 =4,6 10⁴ s ou environ 13 heures.
Méthode d’Euler.
Il est souvent utile de prévoir les courbes de décroissance par une méthode de calcul, la méthode d’Euler par exemple, sans procéder à l’expérience.
À partir de la loi de décroissance A = A₀ e^-lt, l’équation différentielle vérifiée par l’activité A du traceur est :
dA/dt + lA=0.
La méthode d’Euler consiste à introduire les notations suivantes :
dA /dt= DA/Dt pour des intervalles de temps Dt très petits ;
A(t_n+1) = A (t_n) + DA(t_n) avec t_n+1 = t_n + Dt et où Dt est appelé « pas de résolution ».
Montrer que la relation de récurrence entre A(t_n+1) et A(t_n) peut se mettre sous la forme : A(t_n+1) = (1 – l.Dt).A(t_n).
DA(t_n) /Dt=- lA₀e^-lt = -l A(t_n) ; A(t_n+1) = A (t_n) - l A(t_n)Dt =(1 – l.Dt).A(t_n).

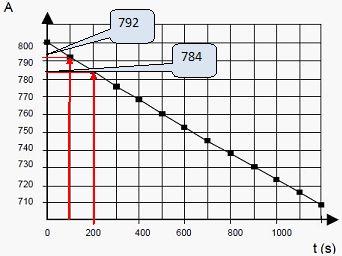
À l’aide de la relation précédente, calculer, pour la dose D₂ de traceur, la valeur en MBq de l’activité A(t₁) à l’instant de date t₁ = 100 s et la valeur de l’activité A(t₂) à l’instant de date t₂ = 200 s et vérifier sur la courbe de la ci-dessous, la validité de ces résultats.
On prendra : A₀ =800 MBq, Dt = 100 s et l = 1.10^-4 s^-1.
A(t₁) = (1 -10^-4*100)*800 =792 MBq.
A(t₂) = (1 -10^-4*100)*792 =784 MBq.

menu