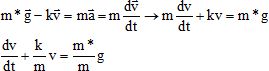Temps
caractéristiques de quelques systèmes
: sujet ASPF ( acueil, savoir, partage, francophonie) 2008
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
| .
. |
|
|
Décroissance radioactive
:
Un échantillon de matière radioactive est placé dans la
chambre d 'un photomultiplicateur. Un détecteur, associé au
photomultiplicateur, mesure un nombre d'événements, pendant une durée Dt déterminée. On trace la courbe d'évolution du
nombre d'événements mesuré par seconde (noté x), au cours du temps.
Soit x0 la valeur de x à l'instant choisi pour origine des
dates. On réalise des mesures avec des échantillons de radon22086Rn
et de radon 22286Rn qui sont des émetteurs a.
Le tableau ci-dessous résume les conditions expérimentales de
cette étude:
|
expérience1
|
expérience 2
|
expérience3
|
|
Grandeurs caractéristiques du système :nature
du
noyau
|
radon 220
|
radon 220
|
radon 222
|
|
Conditions initiales : population initialede
noyaux
radioactifs N0 différent N0' différent N0''
|
N0
|
N0'
|
N0''
|
|
Paramètres extérieurs
|
Aucune modification des paramètres extérieurs
|
|
Temps caractéristique
|
t½ =55,5 s
|
t½ =55,5 s
|
t½ = ??
|
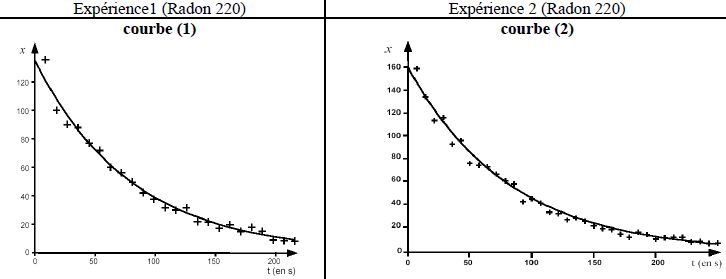
Les courbes correspondant à cette étude et donnant l'évolution
de x au cours du temps sont représentées :
 Définir
le temps de demi-vie (ou demi-vie)
Définir
le temps de demi-vie (ou demi-vie).
La demi-vie ou période est la durée au bout de laquelle la
moitié des noyaux initiaux se sont désintégrés.
La loi de
décroissance radioactive s'écrit sous la forme N
= N0 e-lt
où :
N est le nombre de noyaux radioactifs présents à l'instant de date t, N0
est le nombre de noyaux radioactifs présents à l'instant choisi pour
origine des dates t0 = 0 s, l
est la constante radioactive.
En
utilisant la définition du temps de
demi-vie, établir l'expression de l en
fonction de t½.
½N 0 = N 0 exp (- lt ½) ; ½ = exp (-lt½) ;
ln½ = - lt½ ; - ln 2 = - lt½
; ln2 = lt½.
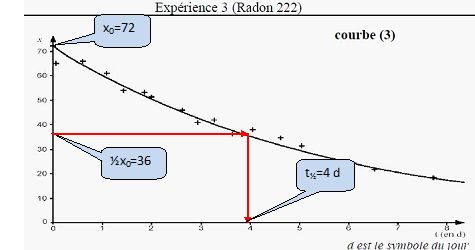
Dans le cas de l'expérience 3, déterminer
graphiquement la
valeur du temps de demi-vie. Pour cette détermination, on admettra que
le nombre d'événements détectés par seconde, à l'instant de date t, est
proportionnel au nombre de noyaux radioactifs présents dans
l'échantillon, à cette méme date. Pour déterminer le temps de demi-vie,
on peut alors utiliser la courbe x = f (t) de la même façon que celle
représentant le nombre de noyaux radioactifs présents dans
l'échantillon en fonction du temps.
 En justifiant les réponses à partir des données du tableau
et du résultat obtenu
En justifiant les réponses à partir des données du tableau
et du résultat obtenu, préciser :
- Si les grandeurs caractéristiques ont une influence sur la valeur du
temps de demi-vie ;
- Si les conditions initiales ont une influence sur la valeur du temps
de demi-vie.
D'après les courbes 1 et 3 ou 2 et 3, t½ dépend de la nature du noyau radioactif.
D'après les courbes 1 et 2, t ½ ne dépend pas du nombre initial de noyaux.
|
|
|
Application de la décroissance radioactive : datation au carbone 14.
En 1983 fut découverte l'épave d'un drakkar dans la vase du port de
Roskilde (à l'ouest de Copenhague). Pour valider l'hypothèse que ce
navire est d'origine viking, une datation au carbone 14 est réalisée
sur un échantillon de bois prélevé sur sa coque. L'activité A mesurée
pour cet échantillon est de 12,0 désintégrations par minute et par
gramme de carbone. Or l'activité pour 1 gramme de carbone participant
au cycle du dioxyde de carbone de l'atmosphère est
A0 = 13,6 désintégrations par minute.
On rappelle que, par définition : A = -dN/dt= l N(t) où N(t) est donné par la loi de décroissance radioactive. La constante radioactive l pour la désintégration du carbone 14 est l = 1,24.10-4 an-1.
Calculer le temps t écoulé entre la date de fabrication du bateau et la date de découverte de l'épave.
A(t)
= A0 e-lt ; ln(A0/A(t) = lt ; t = ln(A0/A(t) / l =ln(13,6 / 12,0) / 1,24.10-4 =1009 ~1,01 103 ans.
Déterminer l'année de construction du bateau.
2008-1009 =999.
La période Viking s'étend du VIIIè siècle au XIème siècle.
L'hypothèse que le bateau est d'origine Viking est-elle vérifiée ?
L'hypothèse d'un bateau d'origine Viking est bien vérifiée.
|
.
|
|
| Chute avec frottements
:
À partir d'une même position de l'espace, on réalise dans deux
fluides différents, la chute verticale sans vitesse initiale de solides
de petites dimensions, de même forme, de même volume, mais de masses
différentes. On filme la chute et un dispositif informatique permet de
tracer la courbe donnant l'évolution de la vitesse v du centre
d'inertie du solide en fonction du temps.
À chaque nouvelle expérience, on ne change qu'une seule des
conditions expérimentales. Le tableau ci-dessous résume les conditions
expérimentales de cette étude :
|
expérience 1 : solide A
|
expérience 2 : solide A
|
expérience 3 : solide B
|
|
Grandeurscaractéristiques du système
|
volume V
|
volume V
|
volume V
|
|
masse m
|
masse m
|
masse m' différente de m
|
|
Conditions initiales :Position initiale,Vitesse
initiale
|
Aucune modification des conditions initiales
|
|
Paramètres extérieurs
|
fluide : eau
|
fluide : détergent
|
fluide : eau
|
|
Temps caractéristique
|
t1 = 0,21 s
|
t2 = 0,15 s
|
t3 = ??
|
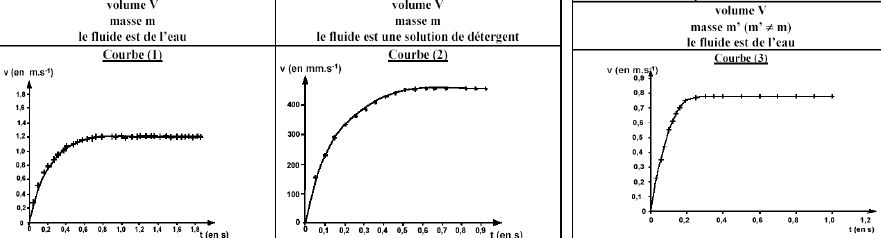
Les courbes correspondant à cette étude et donnant l'évolution de la
vitesse v au cours du temps sont représentées :
Dans le référentiel du laboratoire, supposé galiléen, écrire la 2ème loi de Newton pour le solide de masse m. Ecrire l'équation différentielle vérifiée par la vitesse.
On admettra qu'en présence de fluide, tout se passe comme si le solide
avait un poids m*g < mg (poids apparent, le fluide "porte" le
solide). Le fluide exerce par ailleurs sur le solide une force de
frottement, de la
forme f =kv où est la vitesse du solide et k une constante positive.
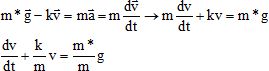
La solution de l'équation différentielle précédente est de la forme : v = vlim(1-e-t/t) où vlim est la vitesse limite atteinte au bout d'un temps très long et t le temps caractéristique de l'évolution.
En utilisant l'équation différentielle du mouvement, déterminer la relation entre vlim et les paramètres k, m* et g.
vlim = constante ; dvlim/dt = 0 : k/m vlim = m*/mg soit vlim = m*g/k.
Déterminer, à partir de l'expression de la fonction v(t), la valeur de la dérivée en t = 0, en fonction de vlim et t.
dvlim/dt =0 = vlim / t e-t/t ; à t=0 : [dvlim/dt]0=vlim / t.
Puis l'équation y(t) de la tangente à la courbe v(t) en t = 0.
y(t) = [dvlim/dt]0 t = vlim / t t.
En déduire une méthode de détermination graphique du temps caractéristique t et le déterminer dans le cas de l’expérience 3. La détermination devra apparaître clairement sur la courbe.
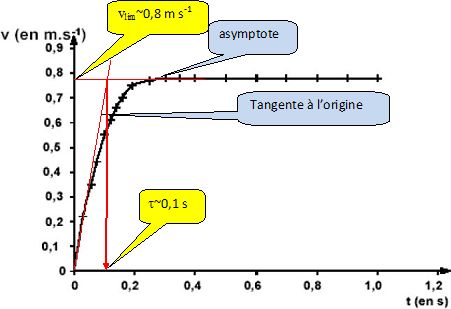
|
|
En justifiant les réponses à partir des données du tableau et du résultat obtenu à la question 13, préciser :
- si les grandeurs caractéristiques ont une influence sur la valeur du temps caractéristique ;
- si les paramètres extérieurs ont une influence sur la valeur du temps caractéristique.
Expériences 1 et 2 : le temps caractéristique dépend de la nature du liquide ( paramètre extérieur ).
Expériences 1 et 3 : le temps caractéristique dépende de la masse m du solide ( grandeur caractéristique).
Lors de la chute verticale d’un solide dans un fluide, le mouvement comporte deux phases :
1- une première phase correspondant au « régime initial » ;
2- une seconde phase correspondant au « régime asymptotique».
En justifiant la réponse, préciser sans calcul la nature du mouvement du centre d’inertie du solide en chute :
1- au cours du régime initial ;
La vitesse croît de zéro à une valeur limite : le mouvement est rectiligne accéléré.
2- au cours du régime asymptotique.
La valeur de la vitesse est constante : le mouvement est rectiligne uniforme.
|
|
|