Statique des fluides, électroaimant, moteur asynchrone. Concours Caplp maths sciences 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . Statique des fluides. Préciser, pour la formule présente dans les capacités du programme les grandeurs et unités mises en jeu. Nommer la loi qu'elle traduit. Loi de la statique des fluides : pA-pB = r g h. pA et pB pression aux points A et B exprimées en pascal ; r : masse volumique du fluide en kg m-3 ; g : intensité de la pesanteur en m s-2 et h : différence de niveau entre A et B exprimée en m. Préciser à l'aide d'un schéma légendé comment l'usage d'un manoscope permet de modèliser le fonctionnement du pressostat. manomètre : appareil de mesure de la pression. Leur principe de fonctionnement utilise soit  la déformation d'une membrane, soit la hauteur d'une colonne de liquide, soit la variation de la résistance électrique d'un cristal pièzo-électrique. manomètre différentiel : il mesure une différence de pression entre un gaz et l'air (par esemple), visualisée sous forme d'une différence de hauteurs d'un liquide dans les branches d'un tube en U. Citer le nom d'un savant qui est à l'origine de "l'expérience ordinaire du vide". Blaise Pascal. Décrire à l'aide d'un schéma annoté cette expérience et donner son interprétation. La hauteur du vif argent ( mercure) est moindre en haut qu'en bas de la montagne ;  la pesanteur et la pression de l'air  sont les seules causes de cette différence de hauteur. Le baromètre de Toricelli est constitué d'un tube de verre bouché à une extrémité, rempli de mercure de masse volumique mHg. On retourne le tube sur une cuve à mercure comme l'indique la figure ci-dessous. L'ensemble est placé à la surface terrestre en un lieu où la pression atmosphérique est P0. Préciser pour le vif argent, son nom actuel, son symbole, sa principale caractéristique physique et les dispositions réglementaires d'usage de ce produit. Le mercure ( Hg) est le seul métal liquide à température ordinaire. Il doit être manipuler dans un endroit muni de système d'aspiration pour capter les vapeurs. Expliquer en quoi l'étude de ce document historique participe à l'initiation à la démarche d'investigation et au développement d'attitudes transversales chez les élèves. Initiation à la démarche expérimentale : Deux théoriques ont cours pour expliquer l'équilibre des liqueurs : - l'orreur du vide ; -  la pesanteur et la pression de l'air sont les seules causes. Seule l'expérience permettra  de retenir la bonne théorie. Attitudes transversales : Lien avec l'histoire des sciences : à quelle époque a vécu B. Pascal ? Lien avec les mathématiques : B. Pascal invente la première machine à calculer, géométrie, probabilités ; Lien avec la physique : hydrostatique. Lien avec la philosophie. . . Phénomène physique mis en oeuvre lors du fonctionnement de l'électrovanne. Expérience 1 : nous entourons le fil isolé parcouru par un courant électrique sur chacune des deux tiges puis nous approchons l'une des extrémités des deux tiges des petits clous en fer. Expérience 2 : nous ouvrons le circuit dans chaque cas. Décrire ce que vous observer dans chaque expérience. Un fil électrique parcouru par un courant se comporte comme un aimant. Cet effet est renforcé par la présence du noyau de fer doux ou d'acier. Cet aimant est temporaire : le fer doux ou l'acier perdent leurs propriétés magnétiques dès que le courant est coupé. Un tel dispositif illustre le principe de l'électroaimant. Réponse d'un élève : la tige d'acier garde son aimantation, c'est à dire elle garde toujours les constituants provenant de l'aimant tandis que la tige de fer les perd lorsqu'on ouvre le circuit. Identifier les erreurs de représentations. Les atomes du fer doux comme de l'acier sont disposés sous formes de petites unités ou domaines : ces derniers s'orientent dans toutes les directions en absence de champ magnétique externe. Leur effet magnétique moyen est nul. De ce fait l'acier et le fer doux ne constituent pas un aimant permanent. En présence d'un champ magnétique externe ( créé par un courant ou par un aimant ), ces domaines s'orientent suivant le champ extérieur. Leurs effets magnétiques s'ajoutent et le fer doux comme l'acier devienent un aimant temporaire. . Moteur asynchtone. Les vecteurs sont écrits en gras et en bleu.  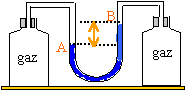Le rotor peut être modèlisé par un circuit filiforme fermé constitué de N spires. L'enroulement total du fil possède une résistance R et une inductance propre L. On note n le vecteur unitaire orthogonal à la surface d'aire S engendrée par l'enroulement ; les vecteurs n et B sont coplanaires tels que ( ux,n) = wt et (ux,B) =wst+a. Exercice bilan proposé aux élèves. Le moteur fonctionne en courant alternatif  ; le rotor en cage d'écureuil est constitué de barres métalliques reliées par deux couronnes ( il est en court-circuit ). L'inducteur créé un champ magnétique qui tourne à la fréquence ns appelée fréquence de synchronisme et exprimée en tour par seconde. 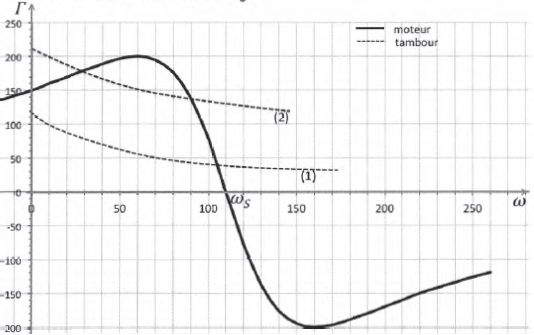Des courants induits naissent dans le rotor ( loi de Faraday ) ; ils créent un couple qui entraîne le rotor à la fréquence de rotation n légèrement inférieure à ns ( loi de Lenz ). Sur le graphique ci-dessous sont représentées les caractéristiques mécaniques d'un moteur et de deux tambours de lave-linge. Rédiger une correction de l'exercice bilan proposé aux élèves. - Identifier les grandeurs représentées sur le graphique en précisant leurs unités. G : moment du couple exprimé en N m ; w : fréquence de rotation exprimée en tour min-1. - Déterminer la nature du moteur. Moteur asynchrone : alimentation en alternatif et la fréquence de rotation du rotor n'est pas exactement celle de la fréquence des courants. - Expliquer à partir du graphique ce qu'il advient si n > ns. Le moteur fonctionne en générateur alternatif. - Préciser la valeur du moment du couple de démarrage de ce moteur. 150 N m ( ordonnée à l'origine ). - Déterminer le moment du couple et la fréquence de rotation au point de fonctionnement du tambour 1. Intersection des deux courbes ( moteur - tambour 1) : G = 40 N m ; w = 105 tours / min. - En déduire la puissance mécanique disponible sur l'arbre du rotor. w = 105*2p /60=~11 rad/s ; puissance mécanique : 40*11 ~4,4 102 W. - Identifier pour le tambour 2 le point de fonctionnement stable et en déduire pour ce cycle la vitesse d'essorage en tr/min. Un système est stable s'il revient à sa position initiale après une perturbation : point de fonctionnement stable  140 Nm ; 90 tr/min. - Expliquer comment modifier la vitesse d'essorage. Ce moteur est alimenté à l'aide d'un onduleur autonome. Enoncer la loi de Faraday. Un circuit fermé traversé par un flux magnétique F ( exprimé en weber ) variable est le siège d'une force électromotrice d'induction e ( exprimée en volt) : e = - dF/dt. Enoncer la loi de Lenz et expliquer pourquoi n < ns. Les courants induits s'opposent par leurs effets électromagnétiques à la cause qui leur donne naissance ( principe de modération ). Ces courants induits sont responsables de l'apparition d'un couple qui met le rotor en mouvement afin de s'opposer à la variation de flux. Si n = ns, il n'y a plus de variation de champ magnétique, ces courants s'annulent, la machine n'est plus entraînée. 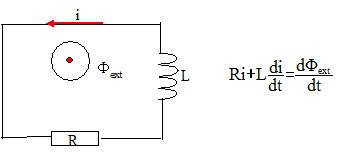Représenter le schéma électrique équivalent du rotor.En déduire une équation où apparaissent l'intensité i du courant induit et le champ magnétique B du stator. Expression de Fext en fonction de t, B0, S, w, ws et a. Fext(t) = B(t) . S(t) avec Bx(t) = B0sin( ws t +a) ; By(t) =B0 cos( ws t+a ) et Sx(t) = S sin( w t ) ; Sy(t) =S cos( w t ) Fext(t) = Bx(t)Sx(t) + By(t)Sy(t) Fext(t) =B0S [sin( ws t +a)sin( wt ) +cos( ws t +a)cos( w t)]=B0S cos(ws-w)t+a). Montrer, par résolution de cette équation en régime établi, qu'en notation complexe le courant i(t) dans le rotor s'écrit i(t) = jSB0W / (R+jLW) exp(j(Wt+a)). On pose W = ws-w ; i(t) = Imax cos(Wt+a+ß) ; ß déphasage de l'intensité par rapport au flux.  Grandeurs complexes associées :  i(t) = Imax exp j(a+ß) ; di/dt = jWImax exp j(a+ß) ; dFext(t)/dt =jWB0S exp ja. L'équation différentielle devient : RImax exp j(a+ß) +LjWImax exp j(a+ß) =jWB0S exp ja. (R+jLW)Imax exp j(a+ß) = jWB0Se xp ja. i(t) =Imax exp j(a+ß) = jWB0S / (R+jLW)exp ja. Par suite en égalant les modules [R2+(LW)2 ] I2 max = (W B0S)2. Imax= W B0S [R2+(LW)2 ] -½ ; si ws=w alors W=0. Si ws=w, il n'y a plus de variation de champ magnétique, ces courants induits s'annulent, la machine n'est plus entraînée. arg  (R+jLW) + ß = arg jWB0S ; ß = ½p-arctan ( LW/R). Exprimer M le moment magnétique du rotor et en déduire la valeur moyenne du moment du couple exercé sur le rotor par les actions mécaniques. M = i(t) S ; G= M ^ B = i (t) S ^ B ; G= i(t) S B0 sin( W t + a) uz. d'où : G= W B20S2 [R2+(Lw)2 ] -½cos(Wt+a+ß) sin( W t + a) uz Expression du couple moyen C=<Gz> en fonction de w, R, L, B0 et S : C=<Gz>=w B20S2 [R2+(Lw)2 ] -½ <cos(Wt+a+ß) sin( W t + a)> Calcul de la valeur moyenne <cos(Wt+a+ß) sin( W t + a)> Or cos(Wt+a+ß) =cos( W t + a)cos ß -sin( W t + a)sin ß et cos(Wt+a) sin( W t + a) =½sin(2( W t + a)). cos(Wt+ß) sin( W t + a) =cos( W t + a)sin( W t + a)cos ß -sin2( W t + a)sin ß =½sin[ 2( W t + a) ]cos ß - sin2((wt+j) sin ß. La valeur moyenne <cos(2Wt+a+ß) > est nulle. La valeur moyenne <sin2((wt+j)> vaut ½. C=<Gz>=W B20S2 [R2+(LW)2 ] -½ ½R /[R2+(Lw)2 ] -½sin ß avec sin ß =R /[R2+(Lw)2 ] -½ . C=½W RB20S2 [R2+(Lw)2 ] -1. .

menu