L'ouie : obtention
d'une mousse, acoustique d'une salle.
Concours Capes 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Obtention d'une mousse métallique pour l'isolation sonore.
Procédé 1 : souflage de gaz dans un métal liquide.
On
observe que pour des bulles de volume uniforme, la transition a lieu
pour une porosité de 74 %. On cherche à interpréter cette valeur limite
de porosité.
En
comparant l'empilement de bulles sphériques à un empilement de sphères
dures, indiquer à quelle situation correspond une porosité de 74 %.
L'empilement compact est un agencement de sphères conduisant à la plus
grande densité de sphères sans que celles-ci se recouvrent. Soit trois
sphères en contact sur un plan A, on peut en placer une quatrième sur
le creux formé par les trois premières. En positionnant des sphères
dans les creux, on obtient un second plan compact B. Cela constitue
l'organisation régulière ayant la plus grande densité.
On retrouve ainsi un empilement dit "hexagonal compact" ou bien
"cubique à faces centrées". Chaque sphère est entourée de 12 autres
sphères et la densité volumique vaut 0,74.
Procédé 2. Décomposition d'un porogène dans le métal liquide.
Le gaz est créé par décomposition d'un solide ( le porogène TiH2) à une température proche de la température de fusion du métal. TiH2 cristallise avec une structure analogue à la fluorine CaF2
: les cations se situent sur les positions caractéristiques d'un
système cubique à faces centrées et les anions occupent tous les
interstices tétraèdriques.
Représenter la maille conventionnelle de l'hydrure de titane.
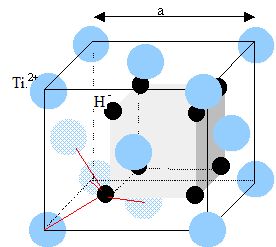 Déterminer le rayon de l'ion hydrure dans cette structure Déterminer le rayon de l'ion hydrure dans cette structure. rTi2+ = 94 pm ; rTiH2 = 3,76 103 kg m-3.
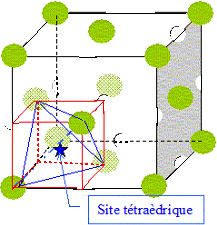
Dimension de la grande diagonale du petit cube rouge ( figure
ci-dessus) :
d2= (½a)2 + (½2½a)2 ; d = 3½
a/2 ; RTi2+ +RH- =½d =3½ a/4.
Il y a 8 anions ( occupant 8 sites tétraèdriques) et 4 cations propres à la maille.
Masse d'un cation : MTi / NA ; masse d'un anion : MH / NA ;
masse des ions dans une maille : m = 8 MH / NA + 4MTi / NA ; volume de la maille : V = a3 ;
masse volumique : rTiH2 = m/V = ( 8 MH / NA + 4MTi / NA) / a3 ;
a=(( 8 MH / NA + 4MTi / NA)/ rTiH2 )1/3 ;
a = ((8 10-3 +4*47,9 10-3)/(6,02 1023*3,76 103))1/3=4,45 10-10 = 445 pm.
RH- =3½ a/4 - RTi2+= 1,73*445/4 -94 =98,7 pm.
|
| .
. |
|
|
La
réaction de décomposition de l'hydrure de titane s'écrit : TiH2(s) ---> Ti(s) + H2(g). K = PH2.
Déterminer la température de décomposition de TiH2(s) sous une pression partielle pH2 = 1,0 bar.
DrH° = -DfH°(TiH2(s))=120 kJ / mol ;
DrS° = S°(Ti(s)) + S°(H2(g)-S°(TiH2(s))=30,7 + 130,7- 29,7 = 131,7 J K-1 mol-1.
DrG° = DrH° -TDrS° = -RT ln K = -RT ln PH2.
Si PH2 = 1 bar, DrG° =0 ; T = DrH° / DrS° =120 103 / 131,7 =911 K ou 638 °C.
Pour obtenir une mousse d'aluminium ( Tf=660 °C), il faut que la température de libération du gaz soit supérieure à la température de fusion du métal. Sous pH2 = 1 bar, on n'obtient pas de mausse d'aluminium.
On souhaite que le dihydrogène soit libéré à 700 °C ( 973 K ).
Déterminer la pression de dihydrogène à soumettre au barreau.
DrH° -TDrS° = -RT ln PH2 ;
ln PH2 =-DrH°/(RT) +DrS° /R =-1,2 105 /(8,32*973) + 131,7 / 8,32 = 1,0 ; pH2 =2,7 bar.
La composition usuelle du barreau est de 5,0 g de TiH2 par
kilogramme d'alluminium. La solidification de la mousse a lieu à 660 °C
sous 1 bar. Dans ces conditions le volume molaire du dihydrogène
est Vm=78 L/mol.
Déterminer la porosité de la mousse.
Volume d'aluminium : 1 / rAl = 1/2700 =3,7 10-4 m3.
Volume de dihydrogène : nTiH2 * Vm = 5,0 / 49,9*0,078 =7,8 10-3 m3.
Porosité = volume du gaz / volume total de la mousse = 7,8 /(7,8 +0,37) =0,95.
|
.
|
|
Acoustique d'une salle.
Dans
une salle de classe les parois réfléchissent partiellement les ondes
sonores. l'énergie incidente sur une paroi est en partie renvoyée vers
la salle, en partie transmise de l'autre côté de la paroi et en partie
absorbée. L'énergie acoustique reçue en un point M provient de la
source S ( énergie directe) et de l'énergie réverbérée par les parois.
L'énergie réverbérée est celle d'un champ sonore, nommé champ diffus,
présent dans toute la salle. On suppose que l'isolation permet de
négliger l'énergie transmise par les parois devant l'énergie absorbée
et réverbérée.
On note ps, la puissance de la source sonore, pabs la puissance absorbée par les parois ; E l'énergie volumique sonore de la salle due au champ diffus ; V le volume de la salle.
Etablir pour une durée dt, un bilan énergétique de la salle.
psdt =EV + pabs dt.
L'énergie absorbée par une paroi dépend du matériau qui la constitue. On définit le coefficient d'absorption a d'un
matériau comme le rapport de la puissance absorbée par une paroi sur la
puissance du champ incident sur celle-ci. L'expérience montre que la
puissance reçue en un point d'une salle suffisamment éloigné de
la source, est pratiquement indépendante de la position du point. Tout
se passe comme si la puissance reçue en un point était égale à la
puissance réverbérée ( hypothèse de Sabine). Cette hypothèse n'est
valable que pour les salles à forte réverbération.
Montrer que dans cette hypothèse, pour une paroi de surface S absorbant une puissance moyenne <pabs>, l'intensité sonore moyenne réverbérée Ir est : Ir = <pabs> / (aS).
<preçue > ~ <pincidente> - <pabs> ; <pabs> = a pincidente ; pincidente = Ir S.
Le produit aS = A se nomme absorption de la salle ou surface équivalente d'absorption.
Caractéristiques de la salle étudiée.
Dimensions : 9,0 m x 7,0 m x 2,5 m. Murs constitués de trois cloisons
en plaques de plâtre et, sur une longueur, d'une façade en béton lisse
peint, vitrée sur 40 % de sa surface. Plafond et sol en béton revêtu.
Estimer le coefficient d'absorption moyen <a> de la salle.
|
a |
Surface (m2) |
aS (m2) |
murs en plâtre
|
0,20
|
(9+7+7)*2,5 =57,5 |
11,5
|
béton lisse
|
0,010
|
9*2,5*0,6=13,5
|
0,135
|
vitres
|
0,030
|
9*2,5*0,4=9
|
0,27
|
plafond et sol
|
0,10
|
2*9*7 = 126
|
12,6
|
Total :
|
24,5
|
Calculer en régime permanent, le niveau sonore réverbéré Lr dans la salle de classe.<ps> = 1,50 µW.
Ir ~<ps> / A = 1,5 10-6 / 24,5 =6,1 10-8 W m-2. Lr = 10 log ( Ir / I0) = 10 log(6,1 10-8 / 10-12)~48 dB.
Comparer
l'intensité sonore réverbérée et celle reçue directement depuis la
source omnidirectionnelle pour un point M situé à d =4 m de la source.
I = <ps> / (4pd2)=1,50 10-6 /(4*3,14*16)~7,5 10-9 W m-2.
I / Ir = 7,5 10-9 /(6,1 10-8 )= 0,12. L'hypothèse de Sabine est bien vérifiée.
|
|
|
Optimisation du temps de réverbération.
Lors
de l'extinction de la source sonore l'intensité acoustique ne s'annule
pas instantanément ; les ondes réverbérées sont amorties et s'éteignent
progressivement. L'enregistrement avec un sonomètre du niveau sonore de
la classe est représenté sur une durée de 1,1 s ( dans la première
partie de la courbe, la source est encore en fonctionnement ).
Le temps de réverbération d'une salle, noté TR, est la durée nécessaire à une décroissance du niveau sonore de 60 dB, après extinction de la source.
Déterminer TR de la clase.
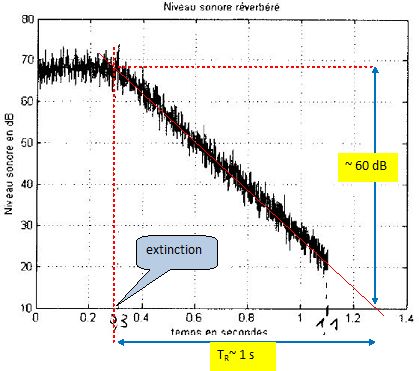
Pour un bon confort acoustique dans une salle de classe, TR doit être compris entre 0,5 et 0,6 s.
Sur quelles parois de la pièce faudrait-il intervenir et en utilisant que matériau ?
TR = 0,16 V/A avec V = 9*7*2,5 = 157,5 m3.
A doit être compris entre 0,16*157,5 / 0,5 = 50,4 et 0,16*157,5 / 0,6 = 42 m2.
Recouvrir le plafond de panneaux fibres vide d'air et la façade de plaque de plâtre.
|
a |
Surface (m2) |
aS (m2) |
murs en plâtre
|
0,20
|
(9+7+7)*2,5 =57,5 |
11,5
|
plaque de plâtre en façade
|
0,20
|
9*2,5*0,6=13,5
|
2,7
|
vitres
|
0,030
|
9*2,5*0,4=9
|
0,27
|
sol
|
0,10
|
9*7 = 63
|
6,3
|
plafond
|
0,41
|
9*7 = 63 |
25,8
|
Total :
|
46,6
|
Quel est l'intérêt d'un faux plafond pour le confort acoustique ?
Un faux plafond acoustique apporte une correction phonique et créé un
vide technique permettant le libre accès aux cables électriques,
dispositifs de ventilation.
|
|
|