Mathématiques : loi de Poisson, loi normale, loi binomiale,
bts
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
Loi
de Poisson.
On désigne par X la variable aléatoire qui, à tout intervalle de temps
d'une durée de 30 s, associe le nombre de skieurs se présentant à une
remontée mécanique, entre 14 h et 15 h. On admet que X suit la loi de
Poisson de paramètre l = 6.
Déterminer
la probabilité P(X=6).
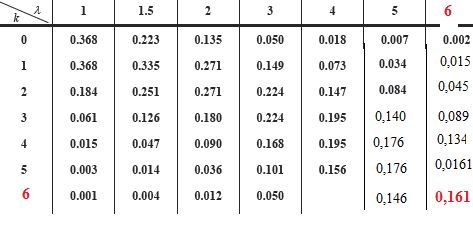
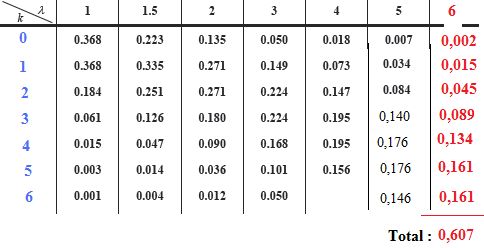
Calculer
la probabilité que, pendant un intervalle de temps d'une durée de 30 s
pris au hasard entre 14 h et 15 h, il se présente au plus 6 skieurs.
P(X=0) +P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6)
Loi normale.
Une entreprise découpe de grande quantité de tubes. Un tube est dit
conforme pour sa longueur ( exprimée en mm ) lorsquelle appartient à
l'intervalle [245 ; 255].
On désigne par Y la variable aléatoire qui, à chaque tube pris au
hasard dans la production d'une journée, associe sa longueur.
Après un réglage de la machine, on admet que la variable aléatoire Y
suit la loi normale de moyenne 250 et d'écart type 3.
Calculer
la probabilité qu'un tube pris au hasard dans la production d'une
journée soit conforme pour sa longueur.
Y suit la loi normale N(m=250, s=3).
p(245<=Y<=255) = p(-5 / 3 <= (Y-m) / s <=5 / 3)
(Y-m) / s suit la loi normale centrée
réduite : 2P(5/3)-1 ~2 P(1,67)-1.
Les tables donnent :

Par suite 2*0,9525-1 =0,905.
Le résultat obtenu n'est pas satisfaisant. On décide de modifier
l'écart type à l'aide d'un nouveau réglage de la machine.
Déterminer l'écart
type pour que P(245 <=Y <=255) = 0,97.
(Y-m) / s suit la loi normale centrée
réduite : 2P(5/s)-1=0,97.
P(5/s)= (1+0,97) / 2 = 0,985.
Les
tables donnent :

5 / s = 2,17 ; écart type s = 5/2,17=2,3.
|
| .
. |
|
|
Loi binomiale.
Dans un lot de tubes, 3 % ne sont pas conformes pour la longueur. On
prélève au hasard 50 tubes de ce lot. Le lot est suffisamment important
pour que l'on puisse assimiler ce prélevement à un tirage avec remise
de 50 lots. On considère la variable aléatoire Z qui a tout prélevement
ainsi défini, associe le nombre de tubes qui ne sont pas conformes pour
la longueur.
Justifier
que Z suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 50. La
probabilité qu'ub tube soit non conforme est constante p = 0,03.
La loi binomiale B(n=50, p = 0,03) est valide.
Calculer
la probabilité P(Z=0).
P(Z=0) = 0,9750 =0,218.
Calculer
la probabilité que dans un tel prélevement au moins un tube ne soit pas
conforme pour la longueur.
1-P(Z=0) = 1-0,218 = 0,782.
|
.
|
|
Loi
normale.
On prélève au hasard une botte de paille dans la production du 20
juillet 2011.
On
désigne par X la variable aléatoire qui, à chaque botte, associe son
épaisseur exprimée en mm. On admet que X suit la loi normale de moyenne
360 et d'écart type 18.
Déterminer
la probabilité P(350 <= X <=370).
X suit la loi normale N(m=360, s=18).
p(350<=X<=370) = p(-10 / 18 < = (X-m) / s <=10 / 18)
(Y-m) / s
suit la loi normale centrée
réduite : 2P(10/18)-1
~2 P(0,56)-1.
Les tables donnent :
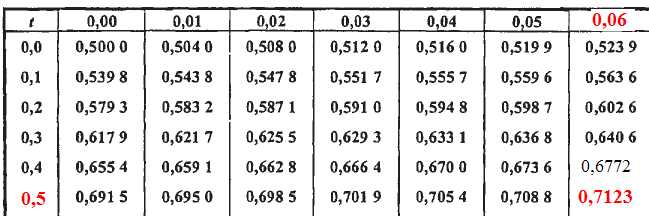
p(350<=X<=370)
=2*0,7123-1 =0,4246 ~0,43.
On
désigne par Y la variable aléatoire qui, à chaque botte, associe sa
densité exprimée en kg m-3. On admet que Y suit
la loi normale de moyenne 100 et d'écart type 5.
Déterminer
la probabilité P(90 <= Y <=110).
Y suit la loi normale
N(m=100, s=5).
p(90<=X<=110) = p(-10 / 5 < = (X-m) / s <=10 / 5)
(Y-m) / s
suit la loi normale centrée
réduite : 2P(2)-1=2*0,9772-1
=0,9544 ~0,95.
On suppose que les variables X et Y sont
indépendantes. Une botte de paille est conforme aux normes d'isolation
si son épaisseur, exprimée en mm, appartient à l'intervalle [350, 370]
et si sa densité, exprimée en kg m-3, appartient
à l'intervalle [90 ; 110 ].
Calculer
la probabilité qu'une botte prélevée dans la production de
cette journée soit conforme aux normes d'isolation.
Les deux varaibles X et Y étant indépendantes : p(conforme) = 0,4246
* 0,9544 =0,4052 ~0,41.
Loi
binomiale.
On considère un stock important de bottes de paille, dont une partie
est destinée à un usage d'isolation. On note E l'évenement " une botte
de paille prélevée au hasard dans le stock est conforme aux normes
d'isolation". On suppose que P(E) = 0,4. On
prélève au hasard 5 bottes de paille dans le stock pour vérification de
la conformité aux normes. Le stock est suffisamment important
pour que l'on puisse assimiler ce prélevement à un tirage avec remise
de 5 bottes. On considère la variable aléatoire Z qui a tout
prélevement
ainsi défini, associe le nombre de bottes qui sont
conformes pour
la longueur.
Justifier
que Z suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 5. La
probabilité qu'une botte soit conforme est constante p = 0,4.
La loi binomiale B(n=5, p = 0,43) est valide.
Calculer
la probabilité P(Z=5). Toutes les bottes sont conformes
aux normes.
P(Z=5) = 0,45 =0,01024 ~0,010.
Calculer
la probabilité que dans un tel prélevement au moins 4 bottes
soient conformes aux normes.
"au moins 4" signifie 4 ou 5.
P(Z=4)=C54 p4
q avec C54
=5*4*3*2 /
(4*3*2)=5 ; p=0,4 et q = 0,6.
P(Z=4)=5*0,44*0,6=0,0768.
P(Z=5)
+P(Z=4)=0,01024
+ 0,0768 ~ 0,087.
Intervalle
de confiance.
On prélève
au hasard 50 bottes de paille dans la production du 22 juillet 2011. La
production est assez importante pour que l'on puisse assimiler ce
prélèvement à un tirage avec remise. On constate que 37 bottes de cet
échantillon sont conformes aux normes.
Donner une
estimation ponctuelle de la fréquence inconnue p des bottes de paille
de cette production qui sont conformes aux normes.
p =37/50 =
0,74.
Soit F la variable aléatoire qui, à tout échantillon de 50 bottes ainsi
prélevé, associe la fréquence des bottes de cet échantillon qui sont
conformes aux normes d'isolation.
On suppose que F suit la loi normale de moyenne inconnue p et d'écart
type s=(p(1-p)/50)½
= (0,74(1-0,74)/50)½
=0,062.
Déterminer
l'intervalle de confiance de la fréquence p au niveau de confiance de
95 % ?
F suit
la loi normale N(p, s).
F0=(F-p)
/ s suit
la loi normale centrée
réduite.
p(-t < F0 < t) =0,95 ; 2P(t)-1 =0,95
; P(t) =1,95/2 =
0,975.
Les tables
donnent t = 1,96.

L'intervalle de confiance est donc : [p-1,96 s ; p+1,96 s ] soit
[0,74-1,96*0,062 ; 0,74+1,96*0,062] ; [
0,62 ; 0,86].
On
considère l'affirmation suivante : " la fréquence p est obligatoirement
dans cet intervalle de confiance".
Cette
affirmation est-elle vraie ?
Cette affirmation est fausse. Dans 95 % des cas, p se trouve
dans cet intervalle de confiance.
|
Loi
normale.
Une
gaine est considérée comme conforme pour le diamètre lorsque le
diamètre intérieur, exprimée en mm, appartient à l'intervalle [8,18 ;
8,48 ].
On
désigne par X la variable aléatoire qui, à chaque gaine prélevée au
hasard dans la production d'une journée, associe son diamètre intérieur.
On admet que X suit la loi normale de moyenne 8,33 et d'écart type 0,09.
Calculer la probabilité qu'une gaine ainsi prélevée soit conforme pour son diamètre intérieur.
X suit la loi normale N(m=8,33, s=0,09).
p(8,18<=X<=8,48) = p(-0,15 / 0,09 < = (X-m) / s <=0,15 / 0,09)
(Y-m) / s
suit la loi normale centrée
réduite : 2P(0,15/0,09)-1
~2 P(1,67)-1.
Les tables donnent :

2*0,9525-1 = 0,905.
Calculer le nombre réel h positif tel que P(8,33-h <= X <=8,33+h) = 0,95 .
2P(t)-1 = 0,95 ; P(t) =1,95/2 =0,975.
Les tables
donnent t = 1,96.

L'intervalle de confiance est donc : [8,33-1,96 s ; 8,33+1,96 s ] soit h = 1,96 s =1,96*0,09 = 0,1764 ~0,176.
La probabilité qu'une gaine ait un diamètre compris 8,33-0,176 =8,15 mm et 8,33+0,176 =8,51mm est 0,95.
Loi
binomiale.
On considère un stock important de bottes de gaines. On note E
l'évenement " une gaine prélevée au hasard dans le stock n'est pas
conforme pour le diamètre inférieur". On suppose que P(E) = 0,096. On
prélève au hasard 50 gaines dans le stock pour vérification du diamètre
intérieur. Le stock est suffisamment important
pour que l'on puisse assimiler ce prélevement à un tirage avec remise
de 50 gaines. On considère la variable aléatoire Y qui a tout
prélevement
ainsi défini, associe le nombre de gaines non
conformes pour
le diamètre intérieur.
Justifier
que Y suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 50.
Chaque
tirage peut déboucher seulement sur 2 résultats : la
probabilité qu'une gaine soit non conforme est constante p = 0,096. La
probabilité qu'une gaine soit conforme est q = 1-p = 0,904.
La loi binomiale B(n=50, p = 0,096) est valide.
Calculer
la probabilité P(Y=5). Dans un tel prélèvement 5 gaines ne sont pas conformes.
P(Y=5)=C505 p5
q45 avec C505
=50*49*48*47*46 /
(5*4*3*2)=2,12 106 ; p=0,096 et q = 0,904.
P(Y=5) = 2,12 106 *0,0965*0,90445= 2,12 106 *8,154 10-6*1,066 10-2 =0,184.
Calculer
la probabilité que dans un tel prélevement au plus deux gaines ne soient pas conformes pour le diamètre intérieur.
"au plus deux" signifie 0, 1 ou 2.
P(Y=0)=C500 p0
q50 avec C500
= 1 ;
P(Y=0)= 0,90650 =7,184 10-3.
P(Y=1)=C501 p1
q49 avec C501
= 50 ;
P(Y=1)=50*0,096* 0,90449 =3,416 10-2.
P(Y=2)=C502 p2
q48 avec C502
= 50*48/2 =1200 ;
P(Y=2)=1200*0,0962* 0,90448 =8,705 10-2.
P(Y=0)
+ P(Y=1) + P(Y=2)= 7,184 10-3
+ 3,416 10-2 + 8,705 10-2~ 0,128
Test d'hypothèse.
On
se propose de construire un test d'hypothèse pour contrôler la moyenne
µ inconnue des diamètres exprimés en mm, d'un lot important de
pastilles de combustible destinées à remplir les gaines. On note D la
variable aléatoire qui, à chaque pastille prélevée au hasard dans le
lot, associe son diamètre. On admet que D suit la loi normale de
moyenne inconnue µ et d'écart type s = 0,2.
On
désigne par D la variable aléatoire qui, à chaque éhantillon
aléatoire de 300 pastilles prélevées dans le lot, associe la
moyenne des diamètres de ces pastilles ( le lot est assez important
pour que l'on puisse assimiler ces prélèvements à des tirages avec
remise ).
L'hypothèse nulle est H0 : µ =8,13. Dans ce cas la livraison est dite conforme pour le diamètre.
L'hypothèse alternative est H1 : µ diffère de 8,13.
Le seuil de signification du test est fixé à 5 %.
Sous l'hypothèse nulle H0, on admet que la variable aléatoire D suit la loi normale de moyenne 8,13 et d'écart type s = 0,012.
On admet également que P(8,106 <= D <=8,154) = 0,95.
Enoncer la règle de décision permettant d'utiliser ce test.
On note d la moyenne des diamètres des pastilles d'un échantillon de 300 pastilles prélevé au hasard avec remise.
Si d appartient à l'intervalle [8,106 ; 8,154 ], on accepte H0 au seuil de 5 %.
Dans le cas contraire, on accepte H1 au risque de 5 %.
On
prélève un échantillon aléatoire de 300 pastilles dans la livraison
reçue et on observe que pour cet échantillon, la moyenne des diamètres
est d = 8,16.
Peut-on, au seuil de 5 %, conclure que la livraison est conforme pour le diamètre.
d n'appartient pas à l'intervalle [8,106 ; 8,154 ] : au risque de 5 %, la livraison n'est pas conforme pour le diamètre.
|
Loi binomiale et loi de Poisson.
On
note E l'évènement " une bouteille prélevée au hasard dans un stock
important est non conforme au cahier des charges". On suppose que la
probabilité de E est p = 0,02.
On prélève au hasard 30 bouteilles
dans le stock pour vérification. On suppose que le stock est
suffisamment important pour qu'on puisse assimiler ce prélèvement à un
tirage avec remise.
On
désigne par X la variable aléatoire qui, à chaque prélèvement de 30 bouteilles, associe le nombre de bouteilles non conformes.
Justifier
que X suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 30.
Chaque
tirage peut déboucher seulement sur 2 résultats : la
probabilité qu'une bouteille soit non conforme est constante p = 0,02. La
probabilité qu'une bouteille soit conforme est q = 1-p = 0,98.
La loi binomiale B(n=30, p = 0,02) est valide.
Calculer P(X <=1).
P(X=0)=C300 p0
q30 avec C300
= 1 ;
P(X=0)= 0,9830 =0,54548.
P(X=1)=C301 p1
q29 avec C301
= 30 ;
P(X=1)=30*0,02* 0,9829 =0,33397.
P(X=0)+
P(X=1) =0,54548 +0,33397 =0,8794 ~0,879.
On considère que la loi de probabilité suivie par la variable aléatoire X peut être approchée par une loi de Poisson.
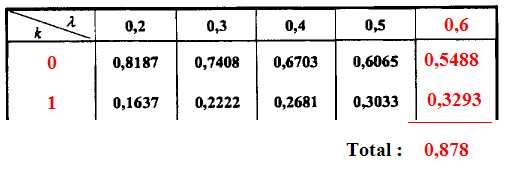
Quel est le paramètre de cette loi de Poisson ? l = np = 30*0,02 =0,6.
On désigne par Y une variable aléatoire suivant a loi de Poisson de paramètre l.
Calculer la probabilité que dans un tel prélèvement de 30 bouteilles, au plus une bouteille soit non conforme.
"au plus une bouteille" signifie 0 ou 1.
Les tables donnent :
Loi normale.
On considère une grande quantité de bouteille devant être livrées à des clients
On
désigne par Z la variable aléatoire qui, à une bouteille prélevée au
hasard dans cette livraison, associe sa contenance en centilitres. On
admet que Z suit la loi normale de moyenne 70 et d'écart type 1.
Déterminer
la probabilité P(68 <= Z <=72).
X suit la loi normale N(m=70, s=1).
p(68<=Z<=72) = p(-2 < = (X-m) / s <=2)
(Y-m) / s
suit la loi normale centrée
réduite : 2P(2)-1.
Les tables donnent P(2)= 0,9772 et 2P(2)-1 = 2*0,9772-1 =0,9544 ~0,95.
Déterminer le nombre réel h positif tel que P(70-h <=Z <=70+h) =0,99.
2P(t)-1 = 0,99 ; P(t) =1,99/2 =0,995.
Les tables
donnent t = 2,575.

L'intervalle de confiance est donc : [70-2,575 s ; 70+2,575 s ] soit h = 2,575 s =2,575*1 = 2,575~2,58.
La probabilité qu'une bouteille est un volume compris 67,4 L et 72,6 cL est 0,99.
Intervalle de confiance.
Une chaine de supermarchés réceptionne un lot important de bouteilles dont elle souhaite estimer la contenance moyenne.
On prélève
au hasard avec remise un échantillon de 100 bouteilles dans ce lot.
Soit C la variable aléatoire qui, à tout échantillon de 100 bouteilles ainsi
prélevé, associe la moyenne des contenance en cL de cet échantillon.
On suppose que C suit la loi normale de moyenne inconnue p et d'écart
type s=0,1.
Pour l'échantillon prélevé, la moyenne est x=70,12.
Déterminer
un intervalle de confiance centré en x de la moyenne µ des contenances
des bouteilles de ce lot, avec le coefficient de confiance de 95 %.
C suit
la loi normale N(p, s).
F0=(F-p)
/ s suit
la loi normale centrée
réduite.
p(-t < F0 < t) =0,95 ; 2P(t)-1 =0,95
; P(t) =1,95/2 =
0,975.
Les tables
donnent t = 1,96.

L'intervalle de confiance est donc : [x-1,96 s ; x+1,96 s ] soit
[70,12-1,96*0,1 ; 70,12+1,96*0,1] soit [ 69,92 ; 70,32].
On
considère l'affirmation suivante : " la moyenne µ est obligatoirement
dans cet intervalle de confiance".
Cette
affirmation est-elle vraie ?
Cette affirmation est fausse. Dans 95 % des cas, µ se trouve
dans cet intervalle de confiance.
|








