Mathématiques : étude d'une fonction, bts
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
Etude
d'une
fonction.
Soit la fonction
définie sur [0 , +oo[ par f(x) = (0,25 x) exp(-0,125 x2).
On désigne par C
la courbe représentative de f dans un repère (O, i, j).
Quelle
est la limite de f(x) quand x tend vers l'infini ?
exp(-0,125
x2)
tend très rapidement vers 0 et 0,25 x tend plus lentement vers l'infini
; l'exponentielle est prépondérante par rapport à 0,25 x : par suite
f(x) tend vers zéro lorsque x devient très grand.
On peut encore dire que la droite d'équation y = 0 est asymptote à la
courbe C quand x tend vers l'infini.
Démontrer
que pour tout réel x de l'intervalle [0 , +oo[,
f
'(x)=0,0625(2+x)(2-x) exp(-0,125x2).
On pose u = 0,25 x et v = exp(-0,125x2).
u' = 0,25 ; v' = -0,25 x
exp(-0,125x2).
Dérivée d'un produit : f '(x) = u' v + v' u
= 0,25exp(-0,125x2)-0,25*0,25 x2
exp(-0,125x2)
f '(x)=0,25
exp(-0,125x2) (1-0,25 x2).
f '(x) =0,25/4 exp(-0,125x2)
(4-0,25*4 x2).
f '(x)= 0,0625 exp(-0,125x2) (4-x2).
f '(x) = 0,0625 exp(-0,125x2)
(2-x)(2+x).
En déduire
le signe
de f'(x) sur [0 , +oo[.
0,0625 exp(-0,125x2) est
toujours positif.
(4-x2)
est positif si x est inférieur à 2 ; (4-x2)
est négatif si x est supérieur à 2.
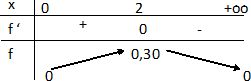
Dresser
le tableau
de variation de la fonction sur [0, +oo[.
Un
logiciel de calcul formel,fournit le développement limité de la
fonction f, à l'ordre 3, au voisinage de zéro :
f(x) = 0,25x-0,031 25 x3 + x3e(x).
En
déduire une
équation de la tangente T à la courbe C au point d'abscisse x=0.
y = 0,25 x.
Etudier la
position
relative de T et C au voisinage du point d'abscisse 0, pour x positif.
Au voisinage de zéro, f(x)-y =-0,031
25 x3 avec x positif.
f(x)-y
est négatif ; f(x) < y : la
tangente est située au dessus de la courbe C.
|
| .
. |
|
|
Etude
locale d'une
fonction.
Soit la fonction définie sur R par f(x) = f(x) = (1-5x) exp(-2x).
On désigne par C la courbe représentative de f dans un repère (O, i, j)
orthogonal.
On admet le résultat suivant : la limite de -5x exp(-2x) vaut zéro
quand x tend vers l'infini.
Quelle
est la limite de f(x) quand x tend vers l'infini ?
-5x
exp(-2x) tend
vers zéro et exp(-2x) tend également
vers zéro quand x devient très grand.
Par suite
f(x) tend vers zéro lorsque x devient très grand.
On peut encore dire que la droite d'équation y = 0 est asymptote à la
courbe C quand x tend vers l'infini.
Le développement
limité à l'ordre 2, au voisinage de zéro, de la fonction h(x) = esp(x)
est :
h(t) = 1 +t +½t2 + t2e(t).
Déterminer
le développement limité, à l'ordre 2, au voisinage de zéro, de la
fonction exp(-2x).
Remplacer t par -2x dans le développement précédent.
g(x) = 1 -2x +2x2
+ x2e(x).
En déduire que le
développement limité, à l'ordre 2, au voisinage de zéro, de
la fonction f est :
f(x) = 1-7x+12x2+ x2e(x).
f(x) = (1-5x) ( 1 -2x +2x2
+ x2e(x)).
f(x) = 1 -2x +2x2
-5x +10x2
+ x2e(x)).
f(x) = 1 -7x +10x2
+ x2e(x)).
En
déduire une équation de la tangente T à la courbe C au point d'abscisse
x=0.
y = 1-7x.
Etudier la
position
relative de T et C au voisinage du point d'abscisse 0, pour x positif.
Au voisinage de zéro, f(x)-y = +10 x2
avec x positif.
f(x)-y
est positif ; f(x) > y : la
tangente est située en dessous de la courbe C.
|
.
|
|
Etude
d'une fonction.
Soit f la fonction définie sur R par f(x) =(2x-1) ex+3.
On note C sa courbe représentative dans le plan muni d'un repère
orthogonal. On admet que la limite de xex est
nulle quand x tend vers moins l'infini.
Calculer
la limite de f(x) quand x tend vers moins l'infini.
f(x) = 2xex-ex+3.
Quand x tend vers moins l'infini :
la limite de 2x ex
vaut zéro ; la limite de ex
vaut zéro ; la limite de f(x) est égale à 3.
On peut encore
dire que la droite d'équation y = 3 est asymptote à la
courbe C quand x tend vers moins l'infini.
En déduire que le
développement limité, à l'ordre 2, au voisinage de zéro, de
la fonction f est :
f(x)=2 + x +1,5 x2+x2e(x).
Le développement
limité à l'ordre 2, au voisinage de
zéro, de la fonction h(x) = ex
est :
h(x) = 1 +x +½x2 + x2e(x).
f(x) =(2x-1) ex+3
= (2x-1)(1 +x +½x2
+ x2e(x))+3.
Développer en se limitant à l'ordre 2 : f(x)= 2x +2x2-1-x-½x2+ x2e(x)+3.
Simplifier : f(x)= 2+x +1,5x2+ x2e(x).
En
déduire une équation de la tangente T à la courbe C au point d'abscisse
x=0.
y = 2+x.
Etudier la
position
relative de T et C au voisinage du point d'abscisse 0.
Au voisinage de zéro, f(x)-y = +1,5 x2 .
f(x)-y
est positif ; f(x) > y : la
tangente est située en dessous de la courbe C.
Etude
d'une fonction.
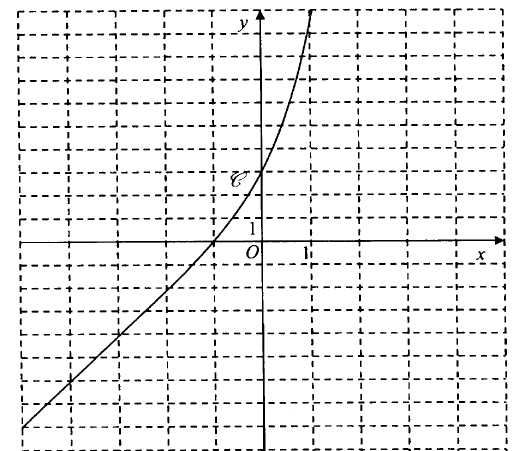
Soit f la fonction définie sur R par f(x) =(1+x)ex +2x+2. On note C sa
courbe représentative dans le plan muni d'un repère orthogonal.
Calculer
la limite de f(x) quand x tend vers l'infini.
Quand x tend vers l'infini :
(1+x)ex tend
vers l'infini ; 2x tend vers l'infini : f(x) tend vers l'infini.
La courbe C admet une asymptote en moins l'infini. Quelle est
son équation ?
Quand x tend vers
moins l'infini : ex tend
vers zéro ; l'exponentielle étant prépondérante devant un polynome :
(1+x)ex tend
vers zéro. La droite d'équation y = 2x+2
est donc asymptote.
Démontrer que le
développement limité, à l'ordre 2, au voisinage de zéro, de
la fonction f est :
f(x)=3 + 4x +1,5 x2+x2e(x).
Le développement
limité à l'ordre 2, au voisinage de
zéro, de la fonction h(x) = ex
est :
h(x) = 1 +x +½x2 + x2e(x).
f(x) =(x+1) ex+2x+2
= (x+1)(1 +x +½x2
+ x2e(x))+2x+2.
Développer en se limitant à l'ordre 2 : f(x)= x +x2+1+x+½x2+ x2e(x)+2x+2.
Simplifier : f(x)= 3+ 4x +1,5x2+ x2e(x).
En
déduire une équation de la tangente T à la courbe C au point d'abscisse
x=0.
y = 3+4x.
Etudier la
position
relative de T et C au voisinage du point d'abscisse 0.
Au voisinage de zéro, f(x)-y = +1,5 x2 .
f(x)-y
est positif ; f(x) > y : la
tangente est située en dessous de la courbe C.
|
.
|