Mathématiques : équation différentielle, étude de fonction, calcul intégral, probabilité ( groupe B), bts 2012.

Mathématiques : équation différentielle, étude de fonction, calcul intégral, probabilité ( groupe B), bts 2011.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

Résolution d'une équation différentielle.
On considère l'équation différentielle (E) : y"-3 y'+2y = -2 e^x+6.
où y est une fonction inconnue de la variable x, définie et dérivable sur R et y' sa fonction dérivée et y" sa dérivée seconde.
Résoudre dans R l'équation : r²-3r+2=0.
Discriminant D = b²-4ac avec a = 1, b= -3 et c=2.
D= 9-4*2 =1 ; D^½ = 1 ; solutions r₁ =(-b +D^½ ) /(2a) =(3+1)/2 = 2 ; r₂ =(-b -D^½ ) /(2a) =(3-1)/2 = 1.
En déduire les solutions de l'équation différentielle (E₀) :
y"-3 y'+2y =0.
y = A e^x+B e^2x avec A et B des constantes réelles.
Soit g la fonction définie sur R par g(x) =2x e^x+3.
Calculer la fonction dérivée g'.
On pose u = 2x ; v = e^x; u' =2 ; v' =e^x ;
Dérivée de 2x e^x : u'v + v'u =2e^x+2x e^x =2e^x (x+1).
La dérivée d'une constante est nulle. Par suite g' = 2e^x (x+1).
Démontrer que la fonction g est une solution particulière de (E).
On pose u = x+1 ; v = 2e^x; u' =1 ; v' =2e^x ;
Dérivée d'un produit : g" = u'v+v'u = 2e^x+2(x+1)e^x =2(x+2)e^x.
Repport dans (E) : 2(x+2)e^x -6e^x (x+1)+2(2x e^x+3) = -2 e^x+6.
Simplifier : -2 e^x+6= -2 e^x+6, égalité vrai quel que soit x.
g(x) est bien une solution de (E).
En déduire l'ensemble des solutions de (E).
Les solutions de (E) sont obtenues en faisant la somme des solutions de (E₀) et d'une solution particulière de (E) :
y = A e^x+B e^2x +2x e^x+3.
Déterminer la solution f de l'équation différentielle (E) qui vérifie les conditions initiales f(0)=2 et f '(0)=1.
f(0) = A e⁰+B e⁰ +3 = A+B+3=2 ; A+B = -1. (1)
f '(x) = A e^x+2B e^2x +2e^x (x+1)
f '(0) =A+2B+2 =1 ; A+2B = -1. (2).
(2)-(1) donne B=0 ; par suite A = -1.
f(x) = - e^x +2x e^x+3 = (2x-1)e^x+3.

.
.

Etude d'une fonction et calcul intégral.
Soit f la fonction définie sur R par f(x) =(2x-1) e^x+3. On note C sa courbe représentative dans le plan muni d'un repère orthogonal. On admet que la limite de xe^x est nulle quand x tend vers moins l'infini.
Calculer la limite de f(x) quand x tend vers moins l'infini.
f(x) = 2xe^x-e^x+3.
Quand x tend vers moins l'infini :
la limite de 2x e^x vaut zéro ; la limite de e^x vaut zéro ; la limite de f(x) est égale à 3.
On peut encore dire que la droite d'équation y = 3 est asymptote à la courbe C quand x tend vers moins l'infini.
En déduire que le développement limité, à l'ordre 2, au voisinage de zéro, de la fonction f est :
f(x)=2 + x +1,5 x²+x²e(x).
Le développement limité à l'ordre 2, au voisinage de zéro, de la fonction h(x) = e^x est :
h(x) = 1 +x +½x² + x²e(x).
f(x) =(2x-1) e^x+3 = (2x-1)(1 +x +½x² + x²e(x))+3.
Développer en se limitant à l'ordre 2 : f(x)= 2x +2x²-1-x-½x²+ x²e(x)+3.
Simplifier : f(x)= 2+x +1,5x²+ x²e(x).
En déduire une équation de la tangente T à la courbe C au point d'abscisse x=0.
y = 2+x.
Etudier la position relative de T et C au voisinage du point d'abscisse 0.
Au voisinage de zéro, f(x)-y = +1,5 x² .
f(x)-y est positif ; f(x) > y : la tangente est située en dessous de la courbe C.

.

On admet que la fonction dérivée de f est donnée, pour tout x réel, par : f '(x) =(2x+1)e^x.
Etudier sur R le signe de f '(x) puis en déduire le sens de variation de f sur R.
e^x est toujours positive ; 2x+1 est négative pour x inférieur à -0,5, nulle pour x=-0,5 et positive pour x supérieur à -0,5.
f '(x) est nulle pour x=-0,5, négative pour x <-0,5 et positive pour x > -0,5.
f(x) est décroissante sur ]-oo ; -½ [ et croissante sur ]-0,5 ; + oo[. La fonction f(x) présente un minimum pour x = -0,5.
Donner la valeur approchée arrondi à 0,01 du minimum de la fonction f.
f(-0,5) =(2*(-0,5)-1) e^-0,5+3 = -2e^-0,5+3 =-2*0,6065 +3 =1,7869 ~1,79.
On note .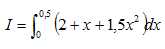
Démontrer que I =1,1875.

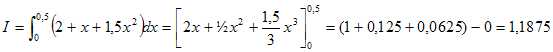
On note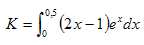
Démontrer, à l'aide d'une intégration par partie, que K= 3-2e^0,5.
On pose : u = 2x-1 ; v ' =e^x ; u'= 2 ; v =e^x.

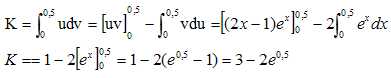
On note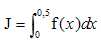
Déterminer la valeur exacte de J.

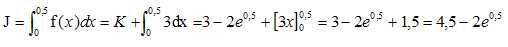
Vérifier que J-I est inférieure à 0,02.
4,5-2e^0,5-1,1875=0,015.

Une entreprise fabrique des bbarres de combustible pour les centrales électriques. des pastilles de combustible sont introduites dans des gaines qui servent à réaliser ces barres.

Loi normale.
Une gaine est considérée comme conforme pour le diamètre lorsque le diamètre intérieur, exprimée en mm, appartient à l'intervalle [8,18 ; 8,48 ].
On désigne par X la variable aléatoire qui, à chaque gaine prélevée au hasard dans la production d'une journée, associe son diamètre intérieur.
On admet que X suit la loi normale de moyenne 8,33 et d'écart type 0,09.
Calculer la probabilité qu'une gaine ainsi prélevée soit conforme pour son diamètre intérieur.
X suit la loi normale N(m=8,33, s=0,09).
p(8,18<=X<=8,48) = p(-0,15 / 0,09 < = (X-m) / s <=0,15 / 0,09)
(Y-m) / s suit la loi normale centrée réduite : 2P(0,15/0,09)-1 ~2 P(1,67)-1.
Les tables donnent :

2*0,9525-1 = 0,905.
Calculer le nombre réel h positif tel que P(8,33-h <= X <=8,33+h) = 0,95 .
2P(t)-1 = 0,95 ; P(t) =1,95/2 =0,975.
Les tables donnent t = 1,96.

L'intervalle de confiance est donc : [8,33-1,96 s ; 8,33+1,96 s ] soit h = 1,96 s =1,96*0,09 = 0,1764 ~0,176.
La probabilité qu'une gaine ait un diamètre compris 8,33-0,176 =8,15 mm et 8,33+0,176 =8,51mm est 0,95.

Loi binomiale.
On considère un stock important de bottes de gaines. On note E l'évenement " une gaine prélevée au hasard dans le stock n'est pas conforme pour le diamètre inférieur". On suppose que P(E) = 0,096. On prélève au hasard 50 gaines dans le stock pour vérification du diamètre intérieur. Le stock est suffisamment important pour que l'on puisse assimiler ce prélevement à un tirage avec remise de 50 gaines. On considère la variable aléatoire Y qui a tout prélevement ainsi défini, associe le nombre de gaines non conformes pour le diamètre intérieur.
Justifier que Y suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 50.
Chaque tirage peut déboucher seulement sur 2 résultats : la probabilité qu'une gaine soit non conforme est constante p = 0,096. La probabilité qu'une gaine soit conforme est q = 1-p = 0,904.
La loi binomiale B(n=50, p = 0,096) est valide.
Calculer la probabilité P(Y=5). Dans un tel prélèvement 5 gaines ne sont pas conformes.
P(Y=5)=C₅₀⁵ p⁵ q⁴⁵ avec C₅₀⁵ =50*49*48*47*46 / (5*4*3*2)=2,12 10⁶ ; p=0,096 et q = 0,904.
P(Y=5) = 2,12 10⁶*0,096⁵*0,904⁴⁵= 2,12 10⁶*8,154 10^-6*1,066 10^-2 =0,184.
Calculer la probabilité que dans un tel prélevement au plus deux gaines ne soient pas conformes pour le diamètre intérieur.
"au plus deux" signifie 0, 1 ou 2.
P(Y=0)=C₅₀⁰ p⁰ q⁵⁰ avec C₅₀⁰ = 1 ; P(Y=0)= 0,906⁵⁰ =7,184 10^-3.
P(Y=1)=C₅₀¹ p¹ q⁴⁹ avec C₅₀¹ = 50 ; P(Y=1)=50*0,096* 0,904⁴⁹ =3,416 10^-2.
P(Y=2)=C₅₀² p² q⁴⁸ avec C₅₀² = 50*48/2 =1200 ; P(Y=2)=1200*0,096²* 0,904⁴⁸ =8,705 10^-2.
P(Y=0) + P(Y=1) + P(Y=2)= 7,184 10^-3 + 3,416 10^-2 + 8,705 10^-2~ 0,128.
Test d'hypothèse.
On se propose de construire un test d'hypothèse pour contrôler la moyenne µ inconnue des diamètres exprimés en mm, d'un lot important de pastilles de combustible destinées à remplir les gaines. On note D la variable aléatoire qui, à chaque pastille prélevée au hasard dans le lot, associe son diamètre. On admet que D suit la loi normale de moyenne inconnue µ et d'écart type s = 0,2.
On désigne par D la variable aléatoire qui, à chaque éhantillon aléatoire de 300 pastilles prélevées dans le lot, associe la moyenne des diamètres de ces pastilles ( le lot est assez important pour que l'on puisse assimiler ces prélèvements à des tirages avec remise ).
L'hypothèse nulle est H₀ : µ =8,13. Dans ce cas la livraison est dite conforme pour le diamètre.
L'hypothèse alternative est H₁ : µ diffère de 8,13.
Le seuil de signification du test est fixé à 5 %.
Sous l'hypothèse nulle H₀, on admet que la variable aléatoire D suit la loi normale de moyenne 8,13 et d'écart type s = 0,012.
On admet également que P(8,106 <= D <=8,154) = 0,95.
Enoncer la règle de décision permettant d'utiliser ce test.
On note d la moyenne des diamètres des pastilles d'un échantillon de 300 pastilles prélevé au hasard avec remise.
Si d appartient à l'intervalle [8,106 ; 8,154 ], on accepte H₀ au seuil de 5 %.
Dans le cas contraire, on accepte H₁ au risque de 5 %.
On prélève un échantillon aléatoire de 300 pastilles dans la livraison reçue et on observe que pour cet échantillon, la moyenne des diamètres est d = 8,16.
Peut-on, au seuil de 5 %, conclure que la livraison est conforme pour le diamètre.
d n'appartient pas à l'intervalle [8,106 ; 8,154 ] : au risque de 5 %, la livraison n'est pas conforme pour le diamètre.

menu