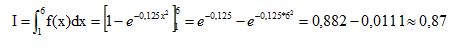Mathématiques : équation différentielle, étude de fonction, probabilité ( groupe B), bts 2013

Mathématiques : équation différentielle, étude de fonction, probabilité ( groupe B), bts 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

Résolution d'une équation différentielle.
On considère l'équation différentielle (E) : y' +(0,25x) y = 0,25 x
où y est une fonction inconnue de la variable x, définie et dérivable sur [0 , +oo[ et y' sa fonction dérivée.
Déterminer les solutions, définies sur [0 ; +oo[ de l'équation différentielle (E₀) :
y' +(0,25x) y =0.
On recherche une solution générale du type : y= A exp(B x²) où A et B sont des constantes.
Dériver : y' = 2AB x exp((B x²).
Repport dans E₀ : 2AB x exp((B x²)+0,25x A exp(B x²)=0.
A x exp(B x²) (2B+0,25) = 0 ; par suite B = -0,125.
y = A exp(-0,125 x²).
Vérifier que la fonction constante h = 1, définie sur [0, +oo[ est une solution de (E).
La dérivée d'une constante est nulle : h'=0 ;
repport dans (E) : 0 +0,25 x =0,25 x est vérifiée quel que soit x.
h=1 est une solution particulière de (E).
En déduire les solutions de (E).
Les solutions de (E) sont obtenues en faisant la somme des solutions de (E₀) et d'une solution particulière de (E) :
y = A exp(-0,125 x²) +1.
Déterminer la solution de l'équation différentielle (E) qui vérifie la condition initiale F(0)=0.
F(0) = A exp(0) +1 = 0 ; A+1 = 0 d'où A = -1.
F = -exp(-0,125 x²) +1.
Etude d'une fonction.
Soit la fonction définie sur [0 , +oo[ par f(x) = (0,25 x) exp(-0,125 x²).
On désigne par C la courbe représentative de f dans un repère (O, i, j).
Quelle est la limite de f(x) quand x tend vers l'infini ?
exp(-0,125 x²) tend très rapidement vers 0 et 0,25 x tend plus lentement vers l'infini ; l'exponentielle est prépondérante pr rapport à 0,25 x : par suite f(x) tend vers zéro lorsque x devient très grand.
On peut encore dire que la droite d'équation y = 0 est asymptote à la courbe C quand x tend vers l'infini.
Démontrer que pour tout réel x de l'intervalle [0 , +oo[, f '(x)=0,0625(2+x)(2-x) exp(-0,125x²).
On pose u = 0,25 x et v = exp(-0,125x²).
u' = 0,25 ; v' = -0,25 x exp(-0,125x²).
Dérivée d'un produit : f '(x) = u' v + v' u = 0,25exp(-0,125x²)-0,25*0,25 x² exp(-0,125x²)
f '(x)=0,25 exp(-0,125x²) (1-0,25 x²).
f '(x) =0,25/4 exp(-0,125x²) (4-0,25*4 x²).
f '(x)= 0,0625 exp(-0,125x²) (4-x²).
f '(x) = 0,0625 exp(-0,125x²) (2-x)(2+x).

.
.

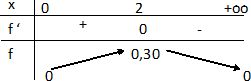
En déduire le signe de f'(x) sur [0 , +oo[.
0,0625 exp(-0,125x²) est toujours positif.
(4-x²) est positif si x est inférieur à 2 ; (4-x²) est négatif si x est supérieur à 2.
Dresser le tableau de variation de la fonction sur [0, +oo[.

Un logiciel de calcul formel,fournit le développement limité de la fonction f, à l'ordre 3, au voisinage de zéro :
f(x) = 0,25x-0,031 25 x³ + x³e(x).
En déduire une équation de la tangente T à la courbe C au point d'abscisse x=0.
y = 0,25 x.
Etudier la position relative de T et C au voisinage du point d'abscisse 0, pour x positif.
Au voisinage de zéro, f(x)-y =-0,031 25 x³ avec x positif.
f(x)-y est négatif ; f(x) < y : la tangente est située au dessus de la courbe C.

.

Application à l'étude de la vitesse du vent.
Soit F la fonction définie sur [0, + oo[ parF(x) =1-exp(-0,125 x²).
Calculer la limite de F(x) quand x tend vers l'infini.
exp(-0,125 x²) tend vers zéro lorsque x devient grand ; F(x) tend vers 1 lorsque x tend vers l'infini.
Démontrer que F est une primitive sur [0, +oo[ de la fonction f(x) =0,25 x exp(-0,125 x²).
F'(x) =0-(-2*0,125 x) exp(-0,125 x²) = 0,25 x exp(-0,125 x²) = f(x).
Calculer .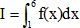

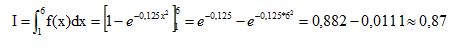
Le résultat précédent donne la probabilité, qu'une journée donnée, la vitesse moyenne du vent soit comprise entre 1 m/s et 6 m/s.
Loi de Poisson.
On désigne par X la variable aléatoire qui, à tout intervalle de temps d'une durée de 30 s, associe le nombre de skieurs se présentant à une remontée mécanique, entre 14 h et 15 h. On admet que X suit la loi de Poisson de paramètre l = 6.
Déterminer la probabilité P(X=6).

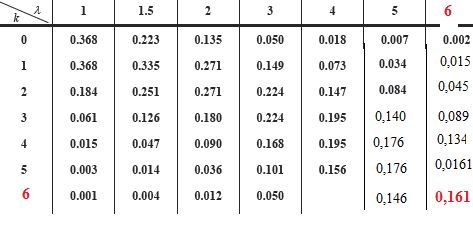
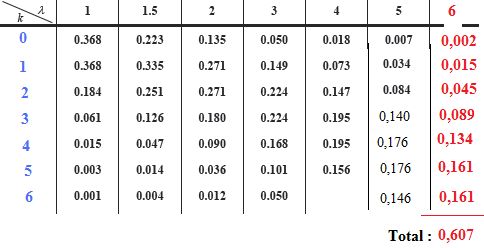
Calculer la probabilité que, pendant un intervalle de temps d'une durée de 30 s pris au hasard entre 14 h et 15 h, il se présente au plus 6 skieurs.
P(X=0) +P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6)

Loi normale.
Une entreprise découpe de grande quantité de tubes. Un tube est dit conforme pour sa longueur ( exprimée en mm ) lorsquelle appartient à l'intervalle [245 ; 255].
On désigne par Y la variable aléatoire qui, à chaque tube pris au hasard dans la production d'une journée, associe sa longueur.
Après un réglage de la machine, on admet que la variable aléatoire Y suit la loi normale de moyenne 250 et d'écart type 3.
Calculer la probabilité qu'un tube pris au hasard dans la production d'une journée soit conforme pour sa longueur.
Y suit la loi normale N(m=250, s=3).
p(245<=Y<=255) = p(-5 / 3 <= (Y-m) / s <=5 / 3)
(Y-m) / s suit la loi normale centrée réduite : 2P(5/3)-1 ~2 P(1,67)-1.
Les tables donnent :

Par suite 2*0,9525-1 =0,905.
Le résultat obtenu n'est pas satisfaisant. On décide de modifier l'écart type à l'aide d'un nouveau réglage de la machine.
Déterminer l'écart type pour que P(245 <=Y <=255) = 0,97.
(Y-m) / s suit la loi normale centrée réduite : 2P(5/s)-1=0,97.
P(5/s)= (1+0,97) / 2 = 0,985.
Les tables donnent :

5 / s = 2,17 ; écart type s = 5/2,17=2,3.
Loi binomiale.
Dans un lot de tubes, 3 % ne sont pas conformes pour la longueur. On prélève au hasard 50 tubes de ce lot. Le lot est suffisamment important pour que l'on puisse assimiler ce prélevement à un tirage avec remise de 50 lots. On considère la variable aléatoire Z qui a tout prélevement ainsi défini, associe le nombre de tubes qui ne sont pas conformes pour la longueur.
Justifier que Z suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 50. La probabilité qu'ub tube soit non conforme est constante p = 0,03.
La loi binomiale B(n=50, p = 0,03) est valide.
Calculer la probabilité P(Z=0).
P(Z=0) = 0,97⁵⁰ =0,218.
Calculer la probabilité que dans un tel prélevement au moins un tube ne soit pas conforme pour la longueur.
1-P(Z=0) = 1-0,218 = 0,782.

Test d'hypothèse.
On se propose de construire un test d'hypothèse pour contrôler la moyenne µ inconnue des longueurs, exprimées en mm, d'un lot important de tubes.
On désigne par L la variable aléatoire qui, a chaque échantillon aléatoire de 50 tubes prémevés au hasard dans ce lot, associe la moyenne des longueurs de ces tubes ( le lot n'est pas suffisamment important pour qu'on puisse assimiler ces prélevements à des tiregas avec remise ).
L'hypothèse nulle est H₀ : µ =250. Dans ce cas on considère que le lot est conforme.
Hypothèse alternative H₁ : µ différent de 250. Le seuil de signification du test est fixé à 5 %.
Sous l'hypothèse H₀, on admet que la variable aléatoire L suit la loi normale de moyenne 250 et d'écart type 0,33.
On admet également que P(249,35 <=L <=250,65) = 0,95.
Enoncer la règle de décision permettant d'utiliser ce test.
On détermine la moyenne puis on vérifie que celle-ci appartient à l'intervalle [249,35 ; 250,65].
On prélève un échantillon aléatoire de 50 tubes dans ce lot et on observe, que pour cet échantillon, la moyenne des longueurs est 250,49.
Peut-on, au seuil de 5 %, conclure que ce lot est conforme ?
Oui, 250,49 appartient à l'intervalle [249,35 ; 250,65].

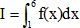menu