Dureté d'une eau, pompe à chaleur,
échanges thermiques : Bts Cira 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
Execice
1.
L'eau
de la rivière qui alimente l'évaporateur d'une pompe à chaleur ne doit
pas être trop dure pour éviter les problèmes dus au dépôt de tartre. Le
dosage de cette eau par une solution d'EDTA permet de déterminer la
concentration totale en ion calcium et magnésium : c0 = [Ca2+]+[Mg2+]=4,0
10-3 mol/L.
Calculer
la dureté de cette eau en degré français.
un
degré correspond à une concentration molaire totale en ions Mg2+ et Ca2+ de 1,0 10-4 mol/L.
La dureté de cette eau est donc : 40 TH. Cette eau est donc qualifiée
de dure.
Un traitement utilisé pour faire chuter ce titre en dessous de 10 °f
est l'utilisation d'une résine échangeuse d'ions de formule simplifiée
RSO3-, Na+. La résine échange ses ions
Na+ avec les ions calcium et magnésium de l'eau à traiter.
Ecrire
les deux équations des réactions d'échange.
2(RSO3-,
Na+ )+ Ca2+ ---> 2RSO3-,
Ca2+ +2Na+.
2(RSO3-,
Na+ )+ Mg2+ ---> 2RSO3-,
Mg2+ +2Na+.
Calculer
la nouvelle concentration molaire c1° = [Ca2+]+[Mg2+] après adoucissement
de cette eau.
TH = 10 °f ; c1° = 10*1,0 10-4 = 1,0 10-3
mol/L.
Le débit de l'eau de rivière étant D =4,0 103 L h-1,
calculer
le nombre total de moles d'ion calcium et magnésium échangé pendant une
heure.
La concentration en ion calcium et magnésium diminue de 3,0 10-3
mol/L.
n = 3,0 10-3 *4,0
103 = 12 mol h-1.
Un
litre de résine échange 2 moles d'ion calcium et magnésium au total en
une heure.
En déduire le volume
de résine utilisé en une heure.
12 / 2 = 6 L.
Exercice
2.
Ecrire l'équation de
la combustion complète du méthane dans l'air.
CH4 g
+ 2O2 g + 8N2 g---> CO2 g + 2H2O
g + 8N2
g
La combustion s'effectuant dans
les conditions stoechiométriques et le débit volumique horaire du
méthane étant égal à qv = 5,0 m3 h-1, calculer :
- le volume de dioxygène utilisé en une heure.
VO2 = 2 Vméthane = 10 m3 h-1.
- le volume d'air correspondant :Vair = 5 VO2 = 50 m3 h-1.
- le pouvoir comburivore du méthane.
C'est le volume d'air nécessaire à la combustion complète de 1 m3
de méthane gazeux.
10 m3 d'air permettent la combustion complète de 1 m3
de méthane.
Calculer
les volumes de dioxyde de carbone et d'eau ( gaz) produits par cette
combustion durant une heure de fonctionnement de la chaudière.
5,0 m3 h-1 de dioxyde de
carbone et 10 m3 h-1 d'eau ( gaz).
En
déduire la masse correspondante de CO2.
nCO2
= VCO2 / Vm = 5,0 / 0,0224 =223,2 mol
Masse de CO2 : nCO2
MCO2 =223,2 *44 =9,8 103 g = 9,8 kg.
Calculer
le pouvoir fumigène humide du méthane.
1+2+8 = 11 m3 de fumées par m3 de méthane.
Pendant une heure de fonctionnement de la chaudière, la masse d'eau
rejetée sous forme de vapeur vaut 8,0 kg.
Calculer
la quantité de chaleur rejetée dans l'atmosphère du fait de la
condensation de la vapeur d'eau.
Lv = 2450 kJ kg-1.
2450*8,0 = 1,96 104 ~2,0 104 kJ.
|
| .
. |
|
|
Pompe à chaleur.
La pompe à chaleur transfère de la chaleur de la rivière à l'eau
destinée au chauffage des bâtiments du groupe scolaire.
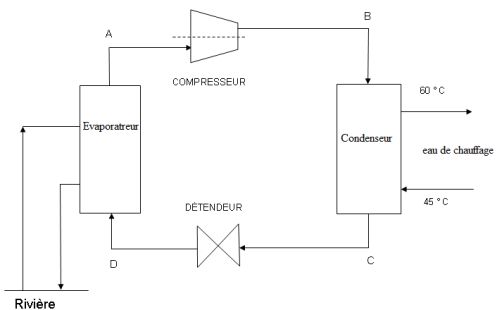
Le fluide
frigorigène est un dérivé de l'éthane. Au départ il se trouve à l'état
de vapeur saturante sèche au point A ( pA = 2 bar ). Il
subit dans un cycle :
une compression isentropique AB jusqu'à la pression pB = 20
bar ;
un refroidissement isobare BC où la vapeur se
refroidit puis se condense totalement à l'état liquide saturant ;
une détente isenthalpique jusqu'au point D ( pD = pA)
;
une évaporation totale isobare jusqu'au point A.
Placer
les points A, B, C et D sur le diagramme de Mollier et en déduire les
enthalpies massiques hA, hB, hC et hD. Quel est l'état
physique du fluide à la sortie du détendeur en D ? Indiquer le titre en
vapeur du fluide.

hA = 390 kJ kg-1 ; hB = 440 kJ kg-1 ; hC =hD=300 kJ kg-1.
En D le fluide est en partie liquide : titre en vapeur en D : 1-0,45 =
0,55.
|
.
|
|
Calculer le travail
massiqueéchangé par le fluide avec le compresseur lors de la
compression AB ?
WAB =hB = hA = 440-390= 50 kJ/kg.
Calculer
la quantité de chaleur massique qBC cédée par le fluide
lors de son refroidissement dans le condenseur.
qBC = hC-hB = 300-440 = -140 kJ kg-1.
Calculer
la quantité de chaleur massique qDA reçue par le fluide
dans l'évaporateur.
qDA = hA-hD
= 390-300 = 90 kJ kg-1.
Définir par une
phrase l'efficacité.
Le
coefficient d'efficacité de la pompe, noté e, est la valeur absolue du
rapport de l'énergie cédée sous forme de chaleur à la source chaude sur
le travail absorbé.
Exprimer
l'efficacité en fonction des variations d'enthalpies et calculer sa
valeur.
e =|qBC|/WAB = 140 / 50=2,8.
Comparer cette
valeur avec l'efficacité eCarnot du cycle de Carnot. TC
= 70°C = 70+273 =343 K et TD = -10°C = -10+273 = 263 K.
eCarnot = TC/(TC-TD)
=343/80~4,3.
Le cycle de Carnot est un modèle théorique où toutes les
transformations sont réversibles. L'efficacité réelle est inférieure à
celle du cycle de Carnot.
En déduire le
rendement thermodynamique : r = e / eCarnot.
r = 2,8 / 4,3 = 0,65.
Echanges thermiques.
Le groupe scolaire dispose d'une chambre froide séparée d'un entrepôt
par une simple cloison en béton. La température de la chambre froide
est constante et vaut qfroide = -15°C ; celle de l'entrepôt vaut qchaud = 18°C et il y règne une humidité relative Hr = 60 %.
Calculer la valeur de la pression de vapeur Pv qui règne à l'intérieir de l'entrepôt.
Psat 18°C = 20,62 mbar ; Hr = Pv / Psat ; Pv = Hr Psat= 0,60*20,62 = 12,37 ~12 mbar. La température de rosée de l'entrepôt vaut 10°C.
Exprimer et calculer la résistance thermique surfacique R de la paroi en béton.
R = ebéton / lbéton + 1/hint + 1 /hext = 0,10 / 0,90 +1/9,0 +1/9,0 = 0,333 ~0,33 m2 W-1K.
Exprimer et calculer la puissance thermique surfacique.
Ptransmise = Dq /R = (18+15)/0,333 =99 W m-2.
En déduire la température intérieure de la cloison du côté entrepôt.
Ptransmise =(qext-qi)h ; qi = qext-Ptransmise / h = 18-99 /9,0 =7°C.
Cette valeur étant inférieure à la température de rosée, il y a condensation de l'eau sur cette paroi.
On isole, du côté entrepôt, avec du polystyrène d'épaisseur epoly = 5,0 cm ( lpoly = 0,04 Wm-1K-1).
Calculer la nouvelle résistance thermique surfacique R1 et la nouvelle puissance transmise.
R1 = R + epoly / lpoly = 0,333 +0,05 / 0,04 =1,583 ~1,6 m2 W-1K.
P'transmise = Dq /R1 = (18+15)/1,583 =20,84 ~21 W m-2.
Y aura-t-il encore condensation de la vapeur d'eau du côté entrepôt.
qi = qext-P'transmise / h = 18-20,84 /9,0 =15,7 ~16°C.
Cette valeur étant supérieure à la température de rosée, il y a pas condensation de l'eau sur cette paroi.
|
|
|

