Etude d'une huile moteur. BTS chimiste 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . L’huile moteur, généralement utilisée pour la lubrification des moteurs à explosion, est une huile minérale, semi-synthétique ou synthétique, dérivée du pétrole et enrichie en additifs techniques. Elle lubrifie, nettoie, inhibe la corrosion, améliore l'étanchéité et contribue à évacuer la chaleur de friction et de combustion (circulation dans les calottes de pistons) de façon à ce que les pièces du moteur restent dans les tolérances de fonctionnement. L’un des paramètres importants pour une huile moteur est la variation de sa viscosité en fonction de sa température : la viscosité à froid ne doit pas être trop élevée pour assurer un bon démarrage (pompage facilité de l’huile) ; la viscosité à chaud (quelques minutes après le démarrage) ne doit pas être trop faible pour continuer à assurer une bonne lubrification du moteur, mais ne doit pas être non plus trop élevée car les frottements défavorisent les économies de carburant. Mesure de la viscosité dynamique à l’aide d’un viscosimètre à chute de bille. Un viscosimètre à chute de bille comporte un long tube, mobile autour d’un axe horizontal. Le tube comporte deux traits repères a et b. La distance entre ces deux repères est notée d. On y introduit de l’huile de masse volumique r et une bille en acier de masse volumique rs et de rayon calibré R tel que son diamètre soit inférieur au diamètre du tube. On rappelle que le volume V d’une sphère de rayon R s’exprime par la relation : V =4/3 pR3. Le tube est muni d’une double enveloppe transparente dans laquelle circule de l’eau provenant d’un bain thermostaté. On rappelle la loi de Stokes pour une bille de rayon R en mouvement à la vitesse v dans un fluide de viscosité dynamique h : la force de frottement est opposée à la vitesse et son expression est : f = 6phRv Déterminer l’unité de la viscosité dynamique à l’aide de la loi de Stokes. h = f /(6pRv). 6 p est sans dimension ; R est une longueur (L) ; v est une vitesse, c'est à dire une longueur divisée par un temps ( LT-1) ; f estbune force soit une masse multipliée par une accélération ( MLT-2). Par suite [h]=MLT-2 / (L2T-1) =ML-1T-1 . ( kg m-1s-1 ou Pa s). Reproduire le schéma simplifié du tube central sur la copie, représenter les forces qui s’exercent sur la bille et les nommer. 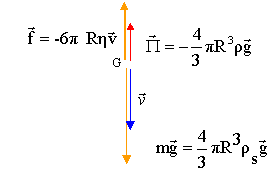La bille est soumise à son poids, à la poussée d'Archimède P et à la force de frottement fluide. . . Expliquer qualitativement pourquoi la bille atteint une vitesse limite. Vérifier que cette vitesse limite a pour expression : vlim=2/9R2g(rs-r)/ h. La poussée d'Archimède et le poids restent constants, tandis que le force de frottement fluide croît avec la vitesse. La bille est pseudo-isolée lorsque la vitesse limite est atteinte : la somme des forces est nulle. 4/3pR3rsg = 4/3pR3rg + 6pRhvlim. 4/3R2rsg - 4/3R2rg = 6hvlim ; vlim= 4/3R2g(rs-r)/ ( 6h)=2/9R2g(rs-r)/ h. Dans les conditions de l’expérience, la bille, lâchée au-dessus du repère, a atteint sa vitesse limite dès le début du mouvement, avant d’atteindre le repère a. Exprimer la vitesse limite de la bille en fonction de d et de Δt, durée de parcours entre les deux repères a et b. vlim = d/Dt. Montrer alors que la viscosité dynamique peut s’écrire sous la forme : h =K(rs-r) Dt. 2/9R2g(rs-r)/ h= d/Dt ; h= 2/9R2g/ d (rs-r) Dt = K(rs-r) Dt. K = 2/9R2g/ d. A 20 °C, on a mesuré une durée de chute Δt = 6,7 s et une masse volumique pour l’huile r = 875 kg.m-3. Calculer la viscosité dynamique de l’huile à cette température. On donne K= 3,55 10-8 Pa m3 kg-1 et rs =7,85 103 kg m-3. h=3,55 10-8( 7,85 103-875)*6,7 =1,66 10-3 Pa s. . Étude de la viscosité dynamique en fonction de la température. On répète la mesure de la durée de chute de la bille à différentes températures afin d’obtenir les valeurs des viscosités dynamiques correspondantes. 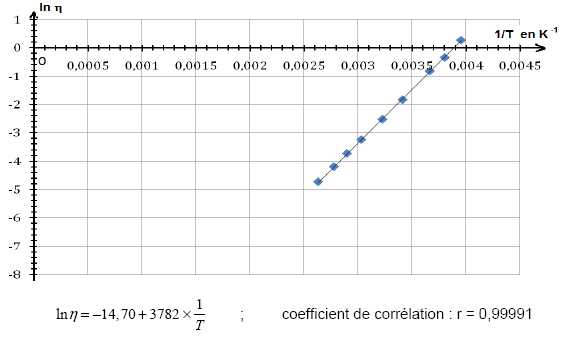Ces valeurs sont regroupées dans le tableau ci-dessous : Viscosité dynamique h( SI) 1,31 0,71 0,44 0,17 8,0 10-2 3,90 10-2 2,4 10-2 1,5 10-2 8,8 10-3 Température ( K) 253 263 273 293 310 330 345 360 380 On trace ln h en fonction de 1/T ; on obtient le graphe et la modélisation ci-dessous : Montrer que cette modélisation vérifie la loi de variation : h =A exp(B/T). ln h = ln A +B/T avec A exprimé en Pa s et B en K.  On identifie ln A =-14,70 et B = 3782 K. L’étude rhéologique de l’huile moteur a été réalisée à 20 °C grâce à un rhéomètre à cylindres coaxiaux. Elle révèle que cette huile a un comportement newtonien. Représenter l’allure du rhéogramme de cette huile. On précisera les grandeurs en abscisse et en ordonnée ainsi que leurs unités. 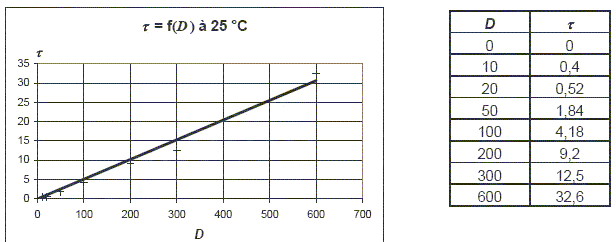t : contrainte de cisaillement exprimée en pascal (Pa) ; D : vitesse de déformation ( seconde-1). Le diagramme est une droite, le comportement du fluide est newtonien. Quelle est la particularité de la viscosité dynamique pour un fluide newtonien ? Si un fluide, à température constante, a une viscosité qui reste constante quelque soit la valeur de la contrainte appliquée, on dit que ce fluide est newtonien Comment déterminer la viscosité dynamique sur ce rhéogramme ? Aucune valeur n’est demandée. Le coefficient directeur de la droite donne la viscosité dynamique du fluide.  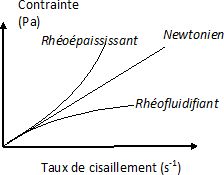Quelle allure le rhéogramme aurait-il pour un fluide rhéofluidifiant ? Même question pour un fluide rhéoépaississant. Comment varie la viscosité dynamique dans chacun de ces deux cas ? Fluide rhéofluidifiant : la viscosité dynamique diminue lorsque le gradient de vitesse augmente. Fluide rhéoépaississant :  la viscosité dynamique augmente lorsque le taux de cisaillement augmente. Quel inconvénient pourrait présenter l’utilisation d’une huile rhéoépaississante pour lubrifier un moteur ? A froid l'huile doit être suffisamment fluide pour démarrer le moteur et amorcer la pompe à huile.

menu