Microscope, spectrophotométrie, thermochimie. Bts bioanalyse et contrôles 2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



.


Observation au microscope.
On se propose d'observer une spore de Penicillium Camemberti à l'aide d'un microscope dont les caractéristiques sont :  objectif, lentille L1 de centre optique O1 et de distance focale f ' 1 = 4,0 mm ; oculaire, lentille L2 de centre optique O2 et de distance focale f ' 2 = 2,0 cm ; intervalle optique D = F'1F2 = 16,0 cm ; distance minimale de vision distincte : dm = 25 cm ; Grossissement commercial du microscope G = Ddm/(f '1 f '2) = a'/a.
Pouvoir de résolution de l'oeil qm = 3 10-4 rad.
Le spore à observer sera noté AB.
Quelle doit être la position de l'image intermédiaire A1B1, de l'objet AB, donnée par L1, pour qu'un observateur puisse observer l'image définitive A'B' à l'infini ?
L'image intermédiaire doit se trouver au foyer objet de l'oculaire.
Quelle est la nature de l'image intermédiaire ? Préciser ses caractéristiques.
L'image intermédiaire est à droite de L1, donc réelle, inversée par rapport à l'objet, plus grande que l'objet.
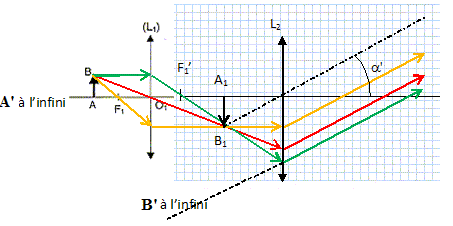
Faire un schéma clair du microscope sans souci d'échelle.

Calculer la valeur du grossissement G.
G = Ddm/(f '1 f '2) =0,160 *0,25 / (0,004*0,02) =500.
Calculer l'angle a sous lequel l'oeil voir à l'oeil nu une spore située à 25 cm de l'oeil.

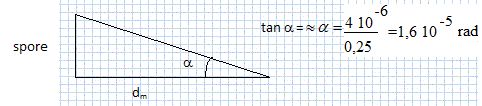Calculer a' .
a' = G a = 500 *1,6 10-5 =8,0 10-3 rad.
Comparer a' et a au pouvoir de résolution de l'oeil et conclure.
a est inférieur au pouvoir de résolution de l'oeil : la spore n'est pas visible à l'oeil nu.
a' est supérieur au pouvoir de résolution de l'oeil : la spore peut être observée à l'aide d'un microsocpe.
Le pouvoir de résolution d'un microscope est limité par la diffraction. La dimension ABmini du plus petit objet observable est donnée par :  ABmini = 1,22 l / (2 n sin u).
l : longueur d'onde de la radiation utilisée ; n sin u : ouverture numérique de l'objectif.
Calculer AB mini si l = 550 nm et u = 60 °. nair = 1,0.
AB mini = 1,22 *550 10-9 / (2*1,0 sin 60 ) =3,87 10-7 m ~3,9 10-7 m.
La spore ayant une dimension de l'ordre de 4 µm, valeur supérieure à ABmini, peut donc être observée au microscope.
u et l étant constantes, justifier l'utilisation d'un bain d'huile pour améliorer le pouvoir séparateur.
L'indice de réfraction de l'huile est supérieur à celui de l'air.
.
.



Spectrophotométrie.
On se propose de contrôler par spectrophotométrie la concentration en permanganate de potassium d'une solution commerciale de liqueur de Dakin ouverte depuis plusieurs semaines. Le spectrophotomètre comporte une source de lumière polychromatique et un réseau possédant 8 105 traits par mètre. Il est muni d'une cuve de longueur l=1 cm.
Donner l'expression de la loi de Beer-Lambert et expliciter chaque grandeur.
La loi de Berr-Lambert exprime la variation de l'intensité lumineuse en fonction de la distance parcourue dans un milieu transparent. Lorsqu'une lumière monochromatique d'intensité I0 traverse un milieu homogène, l'intensité de la lumière émergente I décroît exponentiellement lorsque l'épaisseur l du milieu absorbant augmente.
I = I0 . e (- al)
a est une constante appelée coefficient d'absorption, caractéristique du milieu et de la longueur d'onde considérés.
Dans le cas des solutions, la loi de Beer fait intervenir les concentrations.
I = I0 . e (- elc)
où e est un coefficient caractéristique de la substance appelé coefficient d'absorbance ( m2 mol-1), l est l'épaisseur de la cuve (m) et c la concentration de la solution (mol m-3).
Cette loi est vérifiée lorsque la solution est de concentration inférieure à : c < 0,1 mol.L-1.
La relation fondamentale utilisée en spectrophotométrie est présentée sous la forme :
A= log (I0/I) = elc ( A est l'absorbance ou densité optique)
e est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe.
Indiquer le rôle du réseau.
Le réseau diffracte la lumière polychromatique de la source et permet de sélectionner la longueur d'onde de la lumière qui traverse la solution étudiée.
Justifier le choix de l = 525 nm.
Pour une meilleur précision la longueur d'onde de travail doit correspondre au maximum d'absorption de la solution. La solution de permanganate est violette. L'absorption est maximum pour la couleur complémentaire du violet, c'est à dire le vert jaune ( l = 525 nm).
La mesure de l'absorbance est A = 0,103. En déduire la concentration en permanganate de potassium.
e = 225 mol-1m2 ; l = 0,010 m ; c = A /(el) =0,103 / (225 *0,010) =0,0458 mol m-3 ou 4,58 10-5 mol/L.
Montrer que la concentration massique en permanganate de potassium est 7,24 mg/L.
M(KMnO4 ) = 158 g/mol. Cm =  c M(KMnO4 ) =4,58 10-5 *158 =7,23 10-3 g/L ou 7,23 mg/L.
Calculer l'écart relatif entre Cm et  celle attendue 10 mg/L.Conclure.
(10-7,23) / 10 ~28 %. L'eau de Dakin doit être conservée à l'abri de la lumière sinon elle se décompose rapidement en quelques jours.

.
Synthèse de l'ammoniac  .

Données à 298 K ; R= 8,31 J K-1 mol-1. Les gaz sonr assimilés à des gaz parfaits.
On donne les enthalpies standard de formation et les entropies standard de certains composés chimiques.
Composé
N2 gaz
H2 gaz
NH3 gaz
DfH° (kJ/ mol)
0
0
-46,19
S° (J mol-1 K-1)
191,5
130,6
192,5
pKa(NH4+/NH3)=9,2 ; produit ionique de l'eau Ke = 10-14.
Calculer l'enthalpie standart DrH° de la réaction de synthèse de l'ammoniac à 298 K.
N2(g) + 3 H2(g) = 2NH3(g)
DrH° =2DfH° (NH3(g)) - 3DfH° (H2(g))-DfH° (N2(g)) = 2*(-46,19) = -92,38 kJ.
La réaction est-elle exothermique, endothermique, athermique ? Justifier.
DrH° < 0, la réaction est exothermique.
Calculer l'entropis standard de cette réaction à 298 K.
DrS° =2S° (NH3(g)) - 3S° (H2(g))-S° (N2(g)) = 2*192,5-3*130,6-191,5 = -198,3 J K-1.
Initialement il y a 4 molécules, à la fin il n'y en a plus que 2 : l'ordre augmente ; l'entropie sera donc négative.
Montrer que l'enthalpie standard DrG° associée à cette réaction à 298 K vaut -3,329 104 J mol-1.
DG° = DH°-TDS° = -92,38 103 -298*(-198,3) =-3,329 104 J mol-1.
DrG° <0, cette réaction est thermodynamiquement possible.
Calculer la constante d'équilibre de la réaction à 298 K.
DrG° = -RT ln K
ln K =-(-33,29 103 )/ (8,31*298) =13,44 ; K = 6,86 105.
K est très grand, la réaction dans le sens direct est totale.
Quel est l'influence sur l'équilibre de la réaction
- d'une augmentation de pression  à température constante ?
Lors d'une hausse de pression à température constante et en système fermé, l'équilibre est déplacé dans le direct, c'est à dire diminution du nombre de moles de gaz.
- d'une augmentation de température à pression constante ? Justifier.
Toute hausse de température appliquée à un système fermé en équilibre, maintenu à pression ou encore à volume constant entraîne un déplacement dans le sens indirect , si la réaction exothermique.
Expliquer le choix d'une température de 450 °C pour effectuer la synthèse de l'ammoniac.
La température est un facteur cinétique. Une température trop élévée favorise l'évolution de l'équilibre dans le sens indirect.



.




  

menu