Radioactivité, l'iode 131; traitement de l'eau par floculation : bts
Bioanalyse et contrôle 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
.
.
|
|
|
Radioactivité.
L'iode
a pour numéro atomique Z = 53. L'iode 131 se désintègre par
radioactivité de type ß- et sa demi-vie est t½
= 8 jours. On donne 51Sb ; 52Te
; 53 I ; 54Xe ; 55Cs.
NA = 6,02 1023 mol-1
; masse molaire de l'iode 131 M = 131 g/mol.
Donner la
composition du noyau d'iode 131.
53
protons et 131-53 = 78 neutrons.
Donner la
définition de deux isotopes.
Deux isotopes ne diffèrent que par leurs nombres de neutrons ; ils
possèdent le même numéro atomique.
Ecrire
l'équation de désintégration de l'iode 131 en rappelant les lois
utilisées.
13153I
---> AZX
+0-1e.
Conservation de la charge : 53 = Z-1 d'où Z = 54 ( élément Xe)
Conservation du nombre de nucléons : 131 = A +0.
13153I
---> 13154Xe
+0-1e.
Donner la
loi de décroissance radioactive.
On note N(t) le nombre de noyaux présents à la date t ; N0
: nombre initiaux de noyaux radioactifs ; l : constante
radioactive ( s-1).
N(t) = N0 exp(-l t).
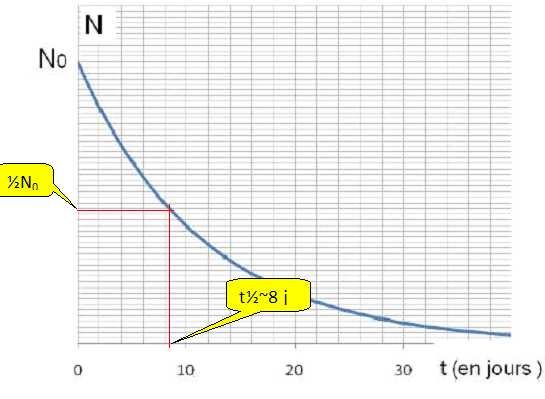
On
souhaite déterminer la demi-vie de l'iode 131. Pour cela, on étudie un
échantillon d'iode 131, on mesure à différentes dates le nombre N de
noyaux d'iode 131 restants. Les résultats obtenus figurent dans le
graphique ci-dessous.
Rappeler
la définition de la demi-vie radioactive. La
déterminer graphiquement.
La demi-vie radioactive est la durée au bout de laquelle l'activité
initiale est divisée par deux.
|
|
|
Retrouver
cette valeur par le calcul.
On donne l
= 1,00 10-6 s-1.
t½ = ln2 / l
= ln2 / (1,00
10-6)
=6,93 105 s ou 8,02 j.
En cas d'accident
nucléaire, les autorités sanitaires conseillent de prendre un comprimé
d'iode stable, l'iode 127.
On
suppose qu'il n'y a plus de danger sanitaire lorsque le nomnre N de
noyaux radioactifs présents a été divisé par 10 par rapport à la
quantité initiale N0 produite au moment de
l'accident. En supposant que le nuage radioactif reste immobile, déterminer
au bout de combien de jours le traitement pourra être arrêté
?
ln(N0
/ N) = l
t ; t = ln10 / l
= ln10 / (1,00
10-6)
= 2,30 106 s ou 26,7 j.
|
.
|
|
Traitement de l'eau par floculation.
L'une
des étapes de traitement des eaux usées est la coagulation /
floculation : elle permet de séparer les petites particules solides
présentes dans l'eau. Les
séparations liquide-solide telles que décantation, sédimentation,
deviennent inefficaces lorsque les particules solides sont trop petites
( dimension inférieure au µm ). Le principe de la coagulation /
floculation est de rassembler les très fines particules contenues dans
l'eau, afin de créer des flocons ou "flocs", particules plus grosses
qui sédimenteront plus facilement. On donne :
g = 9,81 m s-2 ; masse volumique des particules en suspension : r = 1,54 103 kg m-3 ; rayon moyen d'une particule r = 0,80 µm ; masse volumique de l'eau re = 1,00 103 kg m-3 ; viscosité de l'eau à la tempréature de travail h = 1,0 10-3
Pa s. Force de frottement viqueux, qui s'exerce sur une particule
sphérique de rayon r en mouvement à la vitesse v dans l'eau : f = 6p ne r v.
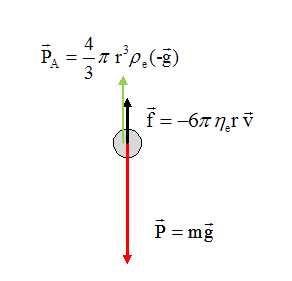
On considère une particule sphérique de masse volumique r
et de rayon r, initialement immobile, en suspension dans l'eau ;
celle-ci acquiert rapidement un mouvement rectiligne. On suppose que la
poussée d'Archimède notée PA s'applique à la particule.
Représenter sur
un schéma, sans souci d'échelle, en les identifiant clairement les
forces appliquées à la particules : poids, poussée d'Archimède et force
de frottement visqueux.
Etablir l'expression littérale de ces forces.
On
constate expérimentalement qu'à partir de l'instant initial, la vitesse
de la particule augmente et atteint très rapidement une limite
constante notée vlim.
Quelle est la nature du mouvement ?
La valeur de la vitesse étant constante, le mouvement est uniforme. De plus il est rectiligne.
Quelle relation vectorielle entre les trois forces peut-on crire lorsque la vitesse a pour valeur vlim ?
Donner la relation entre les expressions des forces s'exerçant sur la particule lorsque la vitesse limite est atteinte.
Montrer que vlim = 2(r-re)r2g / (9he) puis calculer sa valeur.
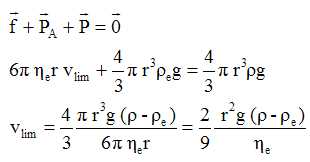
vlim =2*(0,80 10-6)2 *9,81(1,54-1)103/(9*1,0 10-3)=7,5 10-7 m/s.
Quelle est la durée Dt mise par la particule pour parcourur 1,0 cm ? Justifier l'affirmation soulignée dans le texte introductif.
Dt = 1,0 10-2 / vlim =10 10-2 / (7,5 10-7 ) =1,3 104 s ou 3,7 h.
Ces particules très fines sont quasiment immobiles : elles ne seront pas séparées de l'eau par décantation- filtration.
|
On
étudie un "floc" constitué par un groupement d'une centaines de
particules. La grandeur qui est alors modifiée par rapport à l'étude
précédente est le rayon r de la particule. On considère que le "floc"
est de forme sphérique avec un rayon r' = 8 r, la masse volumique
restant inchangée. On note v'lim la vitesse limite du "floc".
Montrer que v'lim / vlim = 64 et expliquer l'intérêt de la floculation dans le traitement des eaux chargées.
La vitesse limite est proportionnelle au carré du rayon de la particule, les autres grandeurs restant inchangées.
vlim = k r2 avec k une constante.
v'lim = k r'2 ; par suite v'lim / vlim =(r'/r)2 = 82 = 64.
v'lim =64*7,5 10-7 = 4,8 10-5 m/s.
Dt '= 1,0 10-2 / v'lim =10 10-2 / (4,8 10-5 ) =2,1 102 s ou 3,4 min.
Les "flocs" peuvent être séparés de l'eau par décantation-filtration.
En dehors de la floculation, la centrifugation est une autre technique fréquemment utilisée.
Expliquer
brièvement son principe, en précisant en particulier quelle grandeur
est modifiée lors de l'utilisation de cette technique.
L'eau
chargée de fines particules est mise en rotation à grande vitesse. Les
particules plus denses que l'eau se trouvent projetées vers l'extérieur
de la centrifugeuse.
En effet leur vitesse v vaut v = wR avec w, vitesse angulaire de la centrifugeuse et R : rayon de le centrifugeuse.
|
|