Etude d'une maison labellisée BBC, éclairage, bts Bâtiment 2013

Etude d'une maison labellisée BBC, éclairage, bts Bâtiment 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

Etude thermique de la maison.
Pour satisfaire le critère BBC, il est conseillé d'avoir, pour les murs, une conductance thermique U_mur < 0,2 W.K^-1.m^-2. On donne :
Enduit : épaisseur e_e = 1 cm, conductivité thermique l_e = 1,15 W.m^-1.K^-1.
Brique : épaisseur e_b = 20 cm, conductivité thermique l_b = 0,11 W.m^-1.K^-1.
Lame d'air : épaisseur e_a = 1,5 cm, conductivité thermique l_a =0,024 W.m^-1.K^-1.
Film mince multicouches : résistance thermique r_mc = 2,5 m².K.W^-1.
Carreau de plâtre : épaisseur e_p = 7 cm, conductivité thermique l_p = 0,46 Wm^-1.K^-1.
La résistance superficielle externe r_se = 0,06 m².K.W^-1.
La résistance superficielle interne r_si= 0,11 m².K.W^-1.
Etude de la résistance thermique des murs.
Les murs d’une habitation ont, de l'extérieur vers l'intérieur, la constitution suivante : une couche d'enduit d’épaisseur 1 cm, de la brique d'épaisseur 20 cm, une lame d'air d'épaisseur 1,5 cm, un film isolant multicouches et des carreaux de plâtre d'épaisseur 7 cm.
Donner l'expression de la résistance thermique surfacique globale d’un mur. Vérifier que la résistance thermique surfacique globale est égale à 5,27 m².K.W^-1.
R_M = r_se +r_si + r_mc + e_e/ l_e+ e_b / l_b + e_a/ l_a+ e_p/l_p.
R_M =0,060 +0,11 +2,5 + 0,01 /1,15 +0,2/0,117 +0,015 /0,024 +0,07 / 0,46 =5,274 ~5,27 m².K.W^-1.
En déduire la valeur de la conductance thermique d’un mur. Cette valeur est-elle compatible avec celle proposée pour le label BBC ?
La conductance est l'inverse de la rsistance soit 1/5,274 =0,1896 ~0,19 W.K^-1.m^-2.
Cette valeur est inférieure à 0,2 W.K^-1.m^-2. la construction respecte le label BBC.
Évaluation des pertes en hiver (environ 60 jours par an).
La température intérieure est de 21 °C et la température extérieure de référence est de -5 °C
Calculer la densité du flux thermique.
j =(q_i-q_f) / R_M =26 / 5,274 =4,93 W m^-2.
La surface totale des murs est de 325 m².
Calculer la puissance thermique perdue à travers ces murs.
P =4,93*325 =1602 W = 1,60 kW
Calculer en kWh, l'énergie consommée pendant la saison hiver.
Dt =60 j = 60*24 =1440 heures.
E = P Dt = 1,60 *1440 =2,31 10³ kWh hiver^-1.

.
.

Évaluation pour les saisons intermédiaires (printemps + automne environ 245 jours).
La température intérieure est de 21 °C et la température extérieure de référence est de 14 °C
Calculer la densité de flux thermique et en déduire la puissance thermique perdue à travers les murs.
j =(q_i-q_f) / R_M =7 / 5,274 =1,3273 ~1,33 W m^-2.
P =1,3273*325 =431,4 W = 0,431 kW
Calculer en kWh, l'énergie consommée pendant les saisons intermédiaires.
Dt =245 j =245*24 =5880 heures.
E = P Dt = 0,431 *5880 =2,54 10³ kWh saisons^-1.
L'ensemble des autres pertes thermiques (fenêtres, baies vitrées, sol, toit, ...) est égal à 4150 kWh par an.
Calculer la consommation énergétique en kilowattheure de cette maison, par mètre carré et par an, sachant que la surface habitable est de 425 m².
E_totale =2,54 10³ +2,31 10³ +4150 =9,0 10³ kWh an^-1.
9,0 10³ /425=21,17 ~21 kWh an^-1m^-2.
Cette valeur étant inférieure à 50 kWh an^-1m^-2, cette construction correspond au label BBC.

.

Etude du chauffage.
Le chauffage de la maison est réalisé par une chaudière au fioul, à condensation, dont le rendement est élevé. Données :
Le pouvoir calorifique supérieur (PCS) du fioul est de 12,8 kWh.kg^-1. La masse volumique du fioul est de 840 kg.m^-3. La masse volumique de l’eau est de 1000 kg.m^-3. Le volume molaire utilisé lors de l’étude est de 24 L.mol^-1.
L’énergie apportée par le fioul domestique utilisé étant de 8000 kWh par an, sachant que le rendement de la chaudière est de 95%, calculer l’énergie utile pour le chauffage.
E_utile = 8000*0,95 =7,6 10³ kWh.
Montrer que la masse de fioul m, consommé par an, est égale à 625 kg. En déduire le volume de fioul consommé par an.
m = E / PCS =8000 / 12,8 =625 kg soit 625/840= 0,744 m³.
On peut assimiler les molécules de fioul à des molécules de formule brute C₂₀H₄₂.
A quelle famille appartient cet hydrocarbure ? Donner la formule brute générale des composés de cette famille.
Les alcanes C_nH_2n+2.
Ecrire l'équation de la combustion complète de ce fioul dans le dioxygène.
C₂₀H₄₂ + 30,5O₂ ---> 20 CO₂ +21 H₂O.
Calculer la quantité de matière, exprimée en moles, de fioul consommé en une année.
M(fioul) = 20*12 +42=282 g/mol = 0,282 kg/mol.
n = m / M(fioul) =625 /0,282 =2,216 10³ ~2,22 10³ mol.
Vérifier que la masse de dioxyde de carbone libéré par cette chaudière pendant une année est égale à 2,0 10³ kg.
n(CO₂) = 20 n = 20*2,216 10³ =4,43 10⁴ mol ; M(CO₂) = 44 g/mol.
Masse de CO₂ : 4,43 10⁴ *44 =1,95 10⁶ g ~2,0 10³ kg.
En déduire la masse de dioxyde de carbone libéré par cette chaudière par mètre carré et par an sachant que la surface habitable est de 425 m². Indiquer le classement de cette maison
pour ce qui est de l'émission de gaz à effet de serre (GES).
2,0 10³ / 425 ~4,6 kg m^-2 an^-1, valeur inférieure à 5, donc classe A.

Eclairage d'une pièce.
L'éclairage à l'intérieur de la maison a été optimisé afin qu'un nombre minimum de lampes assure un éclairage satisfaisant. Dans cette partie, on se propose d'étudier l'éclairage dans une pièce de l'habitation. Pour cela, il sera utilisé le schéma en coupe suivant :

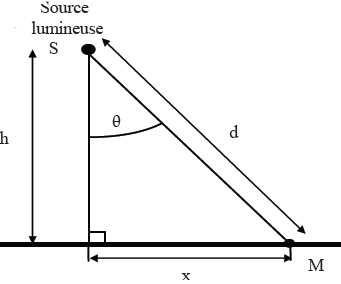
Donner l'expression de l'éclairement E au point M sur une surface horizontale en fonction de la distance d = SM, de l'angle q et de l'intensité lumineuse I de la lampe dans la direction q .
E = I cos q / d².
La lampe utilisée est une lampe halogène de puissance P égale à 1000 W et de flux lumineux F égal à F₀=34000 lumens. Calculer son efficacité lumineuse k.
k = 34000/1000 = 34 lumen W^-1.
Sachant que l'intensité lumineuse I₀ pour une source de Lambert est donnée par la relation I₀= F₀/p, calculer la valeur de cette intensité lumineuse I₀.
I₀ = 34000/3,14 = 1,082 10⁴ ~1,08 10⁴ Candelas.
L'éclairement au point M peut également s'écrire sous la forme : E = I₀h²/(h² +x²)².

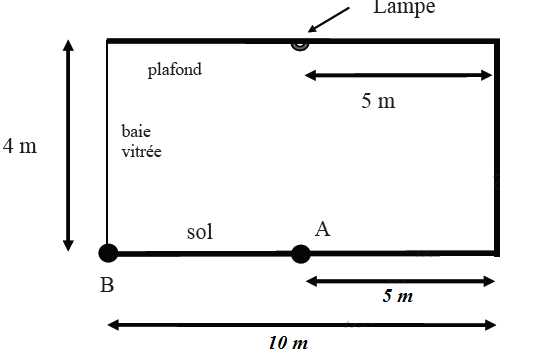
Calculer l'éclairement au point A du sol. (à la verticale de la lampe).
E₀ = I₀/h² =1,082 10⁴ / 16 =6,76 10² lux.
Calculer l'éclairement au point B du sol.
E = I₀h²/(h² +x²)²=1,082 10⁴ *16 / (16+25)² =103 lux.
L'éclairement est considéré comme adapté lorsqu'il est supérieur ou égal à 100 lux. Cette condition est bien satisfaite.

menu