Véhicule électrique : batterie, onduleur, moteur synchrone, CAN : bts AVA 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . La batterie lithium métal polymère. La cellule électrochimique élémentaire de la batterie Lithium Métal Polymère (batterie LMP) est constituée de deux électrodes séparées par un électrolyte polymère solide, conducteur des ions lithium. La cathode est un matériau composé d’oxyde de vanadium. Au cours de la décharge, l’anode, en lithium métallique, produit des ions lithium Li+ qui circulent au sein de la batterie et qui vont vers la cathode. Les caractéristiques des batteries utilisées dans le véhicule étudié sont : · Tension nominale : UN = 400 V · Puissance crête : PC = 45 kW (puissance maximale pouvant être délivrée pendant 30 s ) · Energie massique (ou spécifique) : ρm = 100 W.h.kg-1. · Masse d’une batterie : mB = 300 kg · Quantité d’électricité maximale stockable (capacité) : Q = 75 A.h Déterminer l’énergie chimique ECH stockée dans la batterie LMP en wattheure (W.h), en kilowattheure (kW.h). Energie massique multipliée par la masse : ECH = PC Dt = ρm mB = 100*300 = 3,00 104 Wh ou 30,0 kWh.  L’énergie massique (ou spécifique) d’une batterie au plomb est de l’ordre de 35 W.h.kg-1. Quel est l’intérêt de choisir des batteries du type LMP pour les véhicules électriques plutôt que des batteries classiques au plomb ? A masse égale, les batteries LMP stockent environ 3 fois plus d'énergie que les batteries au plomb, ce qui minimise la masse du véhicule électrique. Réaction à l’anode.  Ecrire la demi-équation électronique de la réaction se produisant à l’anode. Est-ce une réaction d’oxydation ou de réduction ? Justifier. Au cours de la décharge, l’anode, en lithium métallique, produit des ions lithium Li+ , cela correspond à une oxydation du métal lithium avec libération d'électrons. Li(s) = Li+ + e-. La puissance crête est fournie sous la tension nominale. Déterminer l’intensité du courant IC débité par la batterie dans ce cas. PC = UN IC ; IC = PC / UN = 45 103 / 400 =112,5 ~113 A. Pendant combien de temps la batterie pourrait-elle fournir un courant d’intensité égale à I = 15A ? Quantité d’électricité maximale stockable divisée par l'intensité : 75/15 = 5 heures. La batterie est complètement chargée.  Montrer que la capacité de stockage de la batterie est Q = 2,7. 105 C. Q = 75 Ah ou 75 *3600 = 2,7. 105 C. Calculer la quantité de matière d’électrons, exprimée en moles, échangés pendant la décharge complète de la batterie. Donnée : une mole d’électrons a une charge électrique de valeur absolue égale à F = 96500 C n(e-) =2,7. 105 /96500 =2,798 ~2,8 mol.  En déduire la masse de lithium consommé au cours de cette décharge. Donnée : masse molaire atomique du lithium : M(Li) = 6,9 g.mol-1. Li(s) = Li+ + e-. Donc n(Li) = n(e-) =2,798 mol m = n(Li) M(Li) = 2,798 *6,9 = 19,3 ~19 g. . . L'onduleur  autonome de tension. La batterie précédente est branchée sur un onduleur autonome de tension. L’onduleur est un convertisseur statique. Quel type de conversion effectue-t-il ? Conversion courant continu - courant alternatif.  L’onduleur utilise des interrupteurs électroniques. Quelle association de composants électroniques peut jouer ce rôle ? Les interrupteurs électroniques sont constitués d’un transistor et d’une diode en parallèle. On peut réaliser une commande symétrique ou une commande décalée pour l’onduleur ; les chronogrammes respectifs de la tension de sortie sont donnés ci-dessous. Déterminer la période et la fréquence de chacun de ces deux signaux. 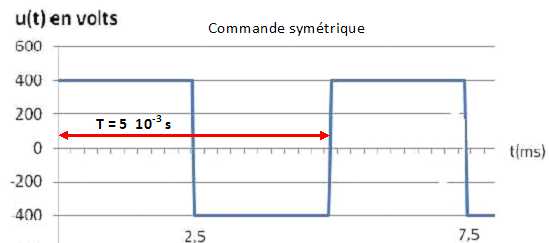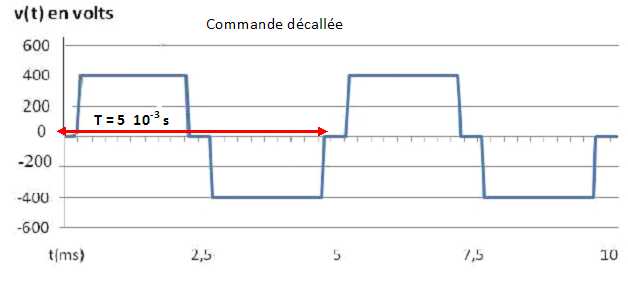f = 1/T = 1/(5 10-3)=1000 / 5 = 200 Hz. . L’analyse spectrale de ces deux tensions de sortie est donnée ci-dessous. Laquelle de ces deux tensions est la plus proche d’une tension sinusoïdale ? Justifier. Déterminer pour chaque tension la fréquence f0 du fondamental (ou harmonique de rang 1) ? 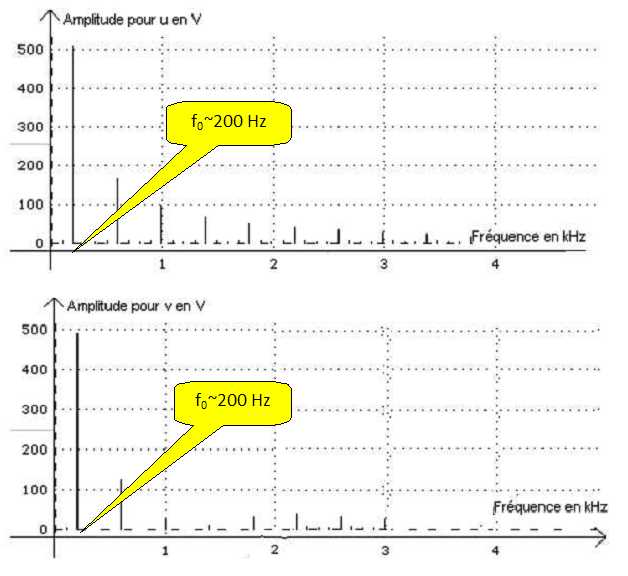Le spectre d'une tension sinusoïdale possède un seul pic, celui du fondamental. Pour la tension v(t) les amplitudes des harmoniques sont assez faibles, celle-ci est plus proche d'une tension sinusoïdale que u(t). Ces tensions présentent-elles des harmoniques pairs ou impairs ? Justifier. Les fréquences des harmoniques sont des multiples de la fréquence du fondamental. Les fréquences des harmoniques sont : 600 = 3*200 Hz ; 1000 = 5*200 Hz ; 1400 = 7*200 Hz .... Les fréquences des harmoniques sont  :(2n+1)f0 avec n entier ou rang de l'harmonique ( harmoniques impaires ).  Donner l’amplitude et la fréquence de l’harmonique de rang 5 de la tension u(t). 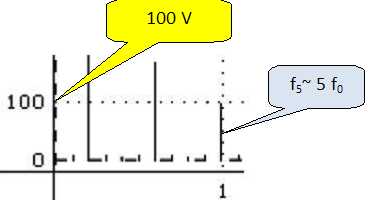Pour alimenter le moteur, on souhaite avoir une tension sinusoïdale ayant la fréquence du fondamental. Quel type de quadripôle peut-on utiliser pour supprimer les harmoniques indésirables ? Préciser la nature et la fréquence de coupure de ce quadripôle. Un filtre passe bas ( association condensateur et résisto ) doit couper les fréquences supérieures à 200 Hz. Mesures des tensions. Quelle est la valeur moyenne de ces deux tensions ? Justifier. Les graphes des tensions étant symétriques par rapport à l'axe des temps, leurs valeurs moyennes sont nulles. Quel appareil doit-on utiliser pour mesurer la valeur moyenne de ces tensions ?  Quelle position du sélecteur de l’appareil de mesure doit-on choisir dans ce cas ? Voltmètre numérique en position DC. Déterminer la valeur efficace U de la tension u(t). La valeur efficace d'un signal carré est égal à sa valeur maximale, soit 400 V. Moteur synchrone. Le véhicule est équipé d’un moteur synchrone. Performances du véhicule données par le constructeur : · Puissance utile maximale du moteur : PU max = 50 kW ; vitesse maximale du véhicule : vmax = 130 km.h-1 ; accélération : 0 à 60 km.h-1 en 6,3 s. Le moteur développe une puissance utile Pu = 30 kW. Le moment du couple moteur est C = 120 N.m.  Calculer sa vitesse angulaire de rotation Ω en rad.s-1. W = Pu / C = 30 103 / 120 =2,5 102 rad/s. En déduire sa fréquence n de rotation exprimée en tr.s-1, en tr/min. 1 tour corespond à 2 p rad : 250/6,28 = 39,8 tr/s ou 39,8*60 =2,387 103 ~2,4 103 tr/min. On se place dans les mêmes conditions que précédemment où le rendement du moteur est égal à : η = 95%. Déterminer la puissance Pa absorbée par le moteur. Pa = Pu/h =30 / 0,95 = 31,6 kW. La masse du véhicule est M = 1,1 t. Déterminer la valeur de l’énergie cinétique du véhicule Ec max, lorsqu’il roule à sa vitesse maximale. 130 km/h = 130/3,6 m/s = 36,1 m/s : Ec max = 0,5 m v2 = 0,5*1100 *36,12 =7,172 105 ~7,2 105 J. Pour s’arrêter sur une route horizontale dans une situation d’urgence, le conducteur freine alors qu’il roulait à la vitesse maximale. En déduire la valeur de l’énergie thermique Q produite au cours de ce freinage. L'énergie cinétique initiale est convertie en énergie thermique au niveau des freins. Q=7,2 105 J. On admet que toute cette énergie Q est échangée avec les disques de frein (en acier). On admet aussi que, le freinage étant suffisamment rapide, il n’y a pas d’échange thermique avec le milieu extérieur. La masse totale des quatre disques est mF = 10 kg. La température initiale des disques de freins est θi = 30°C. Exprimer puis calculer la valeur de la température θf de ces disques à la fin du freinage. Données : la chaleur massique de l’acier est cP = 460 J.kg-1.°C-1. On prendra pour le calcul : Q = 720 kJ. Q = mF cp(qf-qi) ; qf-qi = Q /( mF cp ) ;  qf = qi+Q /( mF cp )= 30 +7,2 105/(10*460)~186°C. Le moteur développe toujours une puissance utile Pu = 30 kW. La vitesse v du véhiculeest de 60 km.h-1. Calculer l’intensité de la force F de traction exercée sur le véhicule. F = Pu / v avec v = 60/3,6 = 16,67 m/s ; F = 30 000 / 16,67 ~1,8 103 N. Conditionnement du signal. Lorsque le véhicule est en mouvement, des capteurs de vitesse inductifs permettent de mesurer la vitesse de rotation des roues. Ils servent à donner l'information électrique « vitesse de roues » au calculateur gérant l’ABS ou l’ESP équipant le véhicule pour effectuer les régulations et éviter le blocage des roues. Le principe des capteurs inductifs est le suivant : la roue qui porte des aimants tourne devant une bobine qui n’est pas alimentée. La roue modifie périodiquement le flux magnétique et donc la tension induite aux bornes de la bobine. Le capteur produit une tension alternative vE dont l’amplitude est fonction de la vitesse de rotation. Afin de pouvoir analyser des tensions faibles, une vitesse de rotation minimale est nécessaire. Le signal de sortie du capteur vE est analogique et doit être conditionné afin que le calculateur puisse traiter son information. Le capteur inductif décrit ci-dessus est-il un capteur actif ou passif ? Justifier. Le capteur inductif est un dipole actif : une partie de la puissance mise en jeu ne correspond pas à de l'effet joule. 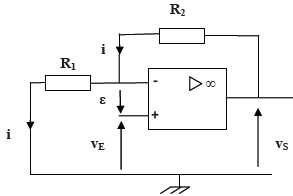On définit l’amplification en tension AV du montage par le rapport : AV = vS/vE. Vérifier que : AV = 1 + R2/R1. e = 0 ; vs = vE +R2i ; vE = R1i ; vS/vE = (R1+R2)/R1 = 1 + R2/R1. La résistance R1 a pour valeur 1 kΩ. Calculer la valeur de la résistance R2 qu’il faut choisir pour obtenir une amplification en tension AV égale à 10. R2 =(Av-1)R1 =9 kW. La tension vs est appliquée à l’entrée d’un CAN qui code sur 11 bits. Que signifient les lettres C, A et N ? Convertisseur Analogique Numérique.  Le CAN fournit un nombre binaire codé sur 11 bits à partir de la tension électrique appliquée à son entrée. Combien de codages différents peut effectuer ce CAN ? 211 =2048. Le CAN est conçu pour qu’on lui applique en entrée une tension comprise entre 0 V et 12 V (sa tension de référence est égale à 12 V). Calculer le pas de quantification (ou quantum) q de ce convertisseur avec trois chiffres significatifs. Le quantum correspond au pas de conversion du CAN et il est calculable par la relation : q =( USmax-USmin) / 2n. Avec n : nombre de bits ; USmax : tension maximale d'entrée du CAN ; USmin : tension minimale d'entrée du CAN. q =12 / 2048 = 5,86 10-3 V =5,86 mV A quels nombres décimaux correspondent les codages binaires suivants : 00000000000 soit 0 en nombre décimal. 11111111111 soit 2048-1 = 2047 en décimal. 00000011111 soit 20 +21+22+23+24 =31 en décimal. Calculer les valeurs des tensions vS correspondant à ces codes binaires. Respectivement 0 V, 12 V et 5,86*32=187,5 mV ~0,187 V. Calculer le nombre de quantum correspondant à une tension vS = 53 mV. En déduire le nombre binaire fourni en sortie du CAN. 53/5,86 ~9,0soit 20+23 ou 1001 en binaire.

menu