Le son : de sa numérisation à la lecture d'un CD : bac S Amérique du Sud 201

Le son : de sa numérisation à la lecture d'un CD : bac S Amérique du Sud 2013

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

Conversion analogique numérique.
Quand on frappe un diapason, il émet un "La" : ses deux branches vibrent pendant quelques secondes à la fréquence f = 440 Hz, entraînant la vibration de l'air qui les entoure. Si on place devant le diapason un micro, la membrane de ce dernier vibre également et ce mouvement est converti en une tenison électrique de même fréquence que le son.

.
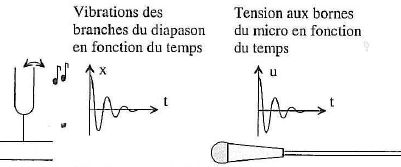Le signal à la sortie du micro est un signal analogique. Justifier brièvement.
Le signal analogique ne présente pas de discontinuité, toutes les valeurs sont possibles.
Un ordinateur ne peut traiter que des signaux numériques.
Définir ce qu'est un signal numérique.
La courbe représentant le signal numérique est un ensemble de fonctions constantes par intervalle, seules quelques valeurs sont possibles. Un signal numérique varie de façon discontinue dans le temps.
Pour traiter un son à l'aide d'un ordinateur, il faut convertir le signal analogique obtenu à la sortie d'un micro en signal numérique : c'est le rôle du convertisseur analogique-numérique ( CAN).
On peut décomposer la conversion en deux étapes : l'échantillonnage et la numérisation. dans la pratique, ces deux étapes se font simultanément.
Que signifie " échantillonner" un signal analogique ?
Echantillonner un signal consiste à capturer des valeurs à intervalles réguliers puis à transmettre celles-ci. L'échantillonnage produit une suite de valeurs discrètes.
Combien de valeurs peut prendre un échantillon numérisé sur 8 bits ?
2⁸ = 256.
Dans le cas d'un CD audio, la numérisation se fait sur 2 x 16 bits ( stéréo ) avec une fréquence d'échantillonnage de 44,1 kHz. Quelle est ( en Mio ) la place théorique occupée sur un CD par une minute de musique non compressée ? 1 octet = 8 bits ; 1 Mio = 2²⁰ octets.
Période de l'échantillonnage : 1 / (44,1 10³) = 2,268 10^-5 s.
Nombre de valeurs obtenues en une minute : 60 / (2,268 10^-5) =2,646 10⁶.
Chaque valeur est codée sur 2*16 bits soit 4 octets.
Nombre d'octets : 4*2,646 10⁶ =1,058 10⁷ soit 1,058 10⁷ / 2²⁰ ~ 10 Mio.

.
.

Lecture d'informations.
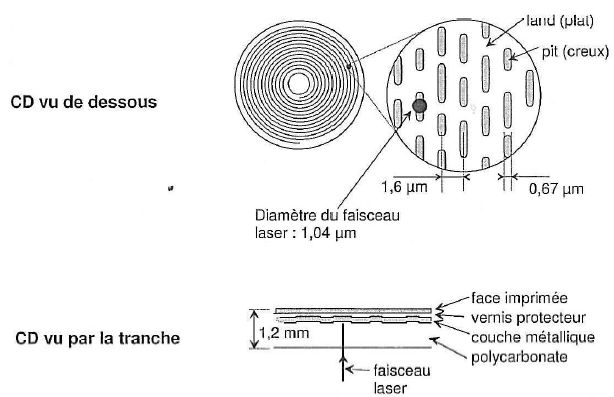
Le CD est en polycarbonate ( matière plastique transparente ) recouvert d'une couche métallique réfléchissante ( aluminium en général ) elle même protégée par un vernis. La face supérieure peut être imprimée ou recouverte d'une étiquette.
les informations sont stockées sous forme de plats ou de cuvettes sur une spirale qui commence sur le bord intérieur d'un CD et finit sur le bord extéroeir. Les creux ont une profondeur de 0,126 µm et une largeur de 0,67 µm.

.

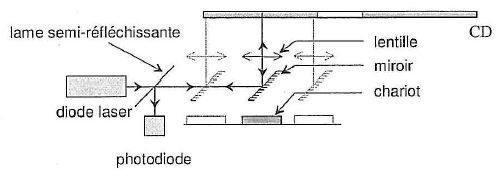
La tête de lecture est constituée d'une diode laser émettant une radiation de longueur d'onde dans le vide l₀ = 780 nm et d'une photodiode détectant la lumière réfléchie par la surface métallisée du CD.
La lumière émise par la diode traverse une lame semi-réfléchissante avant de se réfléchir sur un miroir. La lentille assure la mise au point du faisceau sur le disque. L'ensemble miroir lentille est monté sur un chariot mobile qui permet au faisceau laser de balayer un rayon du disque. La surface du disque défile devant le faisceau laser à une vitesse de 1,2 m/s quelle que soit la position du faisceau.

Le codage de l'information est réalisé par les transitions plat-creux ou l'absence de transition. On donne c = 3,00 10⁸ m/s ; l'indice d'un milieu transparent est défini par la relation n = c / v, v étant la célérité de la lumière dans le milieu transparent.
Citer une propriété du laser iutilisée dans la lecture d'un CD.
La lumière laser est très directive.
Calculer la fréquence de la radiation monochromatique.
f = c / l₀ = 3,00 10⁸ / (780 10^-9)=3,85 10¹⁴ Hz.
L'indice du polycarbonate est n = 1,55. Calculer la célérité de l'onde lumineuse dans le CD.
v = c / n = 3,00 10⁸ /1,55 =1,94 10⁸ m/s.
En déduire la longueur d'onde l de la lumière dans le polycarbonate sachant que la fréquence ne dépend pas du milieu traversé.
l = v / f = l₀ / n = 780/1,55 = 503 nm.
Quand le faisceau laser frappe une cuvette, une partie du faisceau est réfléchie par le fond de la cuvette et le reste par le bord car le diamètre du faisceau est plus grand que la largeur de la cuvette. Ces ondes réfléchies peuvent interférer.

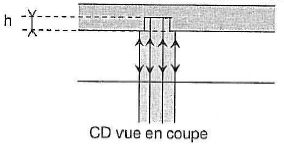
Expliquer pourquoi les interférences sont destructives si h = 0,25 l.
La différence de marche entre les ondes réfléchies par le fond de la cuvette et par le bord est égale à 2 h soit 0,5 l.
les interférences sont destructives si cette différence de marche est un multiple impair de la demi-longueur d'onde.
Vérifier que la profondeur d'une cuvette est bien choisie pour produire des interférences destructives.
0,25 l = 0,25 *503 ~126 nm = 0,126 µm. Les creux ont une profondeur h = 0,126 µm.
Comparer sans calcul l'éclairement de la photodiode quand le faisceau laser éclaire un plat ou une cuvette.
Lors de la détection d'un 1, le faisceau laser passe d'un plat à un creux ou inversement. Une partie du faisceau est alors réfléchie par un plat et l'autre par un creux. Tous les rayons composant le faisceau n'ont pas parcouru le même trajet.
Lors de la détection d'un zéro, le faisceau est entièrement réfléchi par un plat ou par un creux. Touts les rayons composant le faisceau ont donc parcouru le même trajet. Les interférences sont constructives et l'éclairement de la photodiode est maximal.

Lecteur Blu-ray.
On trouve depuis quelques années dans le commerce des lecteurs " Blu-ray" qui utilisent une diode laser bleue dont la longueur d'onde ( l₀ = 405 nm ) est pratiquement égale à la moitié de celle des lecteurs classiques. Les disques Blu-ray peuvent stocker une quantité de données beaucoup plus importante : jusqu'à 25 Go.
Quel est le phénomène physique propre aux ondes qui empêche d'obtenir un faisceau de diamètre plus petit sur le CD ?
La diffraction par un obstacle dont les dimensions sont de l'ordre de grandeur de la longueur d'onde du faisceau.
Expliquer pourquoi l'utilisation d'une diode laser bleue peut permettre de stocker plus d'informations sur un disque Blu-ray dont la surface est identique à celle d'un CD ?
La finesse de la gravure est de l'ordre de grandeur de la longueur d'onde et la distance entre deux "rayons" de la spirale est voisine deux longueur d'onde. En diminuant celle-ci, on augmente la quantité de données gravées.
Doit-on conserver sur un disque Blu-ray, la même profondeur de cuvette que sur un CD classique ? Justifier.
La profondeur de la gravure doit être égale à 0,25 l : en modifiant la longueur d'onde de la lumière, on doit changer la profondeur des cuvettes.
Peut-on lire un CD sur un lecteur Blu-ray ? Une seule justification est demandée.
Non : la largeur du faisceau laser et la profondeur des cuvettes sont différentes.

menu