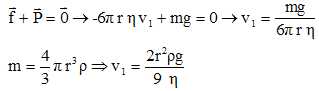Les
débuts de l'électron en physique. Bac S Liban 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
L'expérience
de J.J.Thomson.
Thomson conçoit un dispositif dans lequel un faisceau d'électrons
est dévié lors de son passage entre deux plaques où règne un
champ électrique. La mesure de la déviation du faisceau d'électrons lui
permet de déterminer le rapport e/me.
L'étude suivante porte sur le mouvement d'un électron du faisceau qui
pénètre entre deux plaques parallèles et horizontales P1
et P2, dans une zone où règne un champ
électrique E supposé uniforme et perpendiculaire aux deux plaques. A
l'instant t=0, l'électron arrive en O avec une vitesse horizontale v0.
Le poids des
électrons est négligeable devant la force électrostatique.
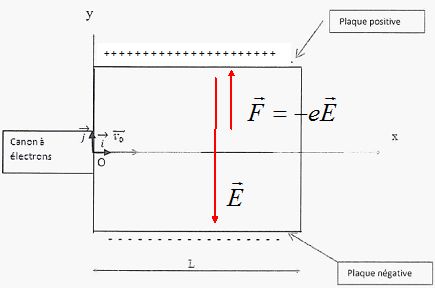
Représenter
le vecteur correspondant au champ électrostatique et celui correspondant à la force électrostatique.
Le vecteur champ électrique pointe vers le plus petit potentiel, celui de la plaque négative.
Le vecteur force et le vecteur champ électrique sont colinéaires et de sens contraire, la charge de l'électron étant négative.
En appliquant la seconde loi de Newton à l'électron, déterminer les équations horaires x(t) et y(t) du mouvement de l'électron.
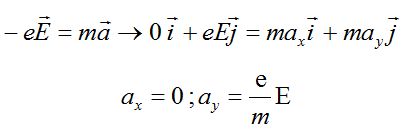
La vitesse est une primitive de l'accélération : vx = v0 ; vy = eE/m t.
La position est une primitive de la vitesse et l'électron est à l'origine du repère à t=0.
x(t) = v0 t ; y(t) = ½eE/mt2.
Vérifier que la trajectoire de l'électron a pour équation y = eEt2/(2mv02).
t = x/v0, repport dans y : y = eEx2/(2mv02).
A la sortie de la zone entre les plaques P1 et P2, l'électron a subit une déviation verticale SH = 2,0 10-2 m.
Longueur des plaques L = 9,0 10-2 m ; v0 = 2,4 107 m/s ; E = 1,6 104 V m-1.
Déterminer la valeur du rapport e/me et conclure.
SH = eEL2/(2mv02) ; e/m = 2SHv02 / (EL2)=2*2,0 10-2 *(2,4 107)2 / (1,6 104 *(9,0 10-2)2)=1,77 1011 ~1,8 1011C kg-1.
Valeur réelle : 1,6 10-19 / (9,1 10-31) =1,76 1011C kg-1.
La valeur expérimentale différe très peu de la valeur réelle ( ~1%).
|
| .
. |
|
|
Description d'une expérience menée de nos jours en laboratoire ( Milikan).
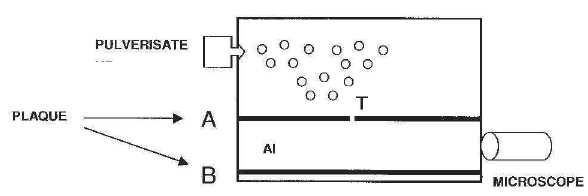 Un
pulvérisateur produit un nuage de gouttelettes d'huile chargées
négativement qui tombent dans la chambre supérieure du dispositif.
Lorsque l'une d'elles passe à travers le trou T, elle tombe
verticalement à une vitesse constante v1, son poids étant
très vite compensé par la force de frottement exercée par l'air. Lors
de cette première étape, la chute verticale de la gouttelette dans
l'air en l'absence de champ électrique est observée à l'aide d'un
microscope et permet de déterminer le rayon r de la gouttelette qui
n'est pas mesurable directement.
Lors d'une deuxième étape, lorsque
la gouttelette parvient en bas du dispositif, un champ électrique
uniforme est créé entre les plaques A et B. La gouttelette remonte
alors verticalement à une vitesse constante v2. La charge électrique portée par la gouttelette est ensuite déduite des mesures des vitesses v1 et v2.
|
.
|
|
La gouttelette de masse m et de charge q négative arrive entre les
plaques A et B. La poussée d'Archimède est négligée. La gouttelette
étudiée est soumise à son poids P et à la force de
frottement f exercée par l'air s'exprimant par la relation 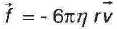 dans laquelle h est la viscosité de l'air, r le rayon de la gouttelette et v sa vitesse. dans laquelle h est la viscosité de l'air, r le rayon de la gouttelette et v sa vitesse.
Masse volumique de l'huile r = 980 kg m-3 ; g = 9, 8 N kg-1 ; h = 1,8 10-5 kg m-1 s-1.
Chute verticale de la gouttelette en absence de champ électrique.
Ecrire
la relation vectorielle entre la force de frottement et le poids
lorsque la vitese constante est atteinte. En déduire l'expression de v1 en fonction de h, r, m et g.
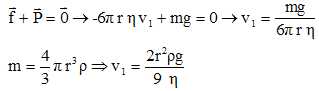
Calculer r sachant que la gouttelette parcourt 2,11 mm en 10,0 s.
v1 = 2,11 10-3 / 10,0 = 2,11 10-4 m s-1.
r = (9v1 h /((2rg))½ =(9*2,11 10-4 *1,8 10-5 /(2*980*9,8))½ =1,334 10-6 m ~1,3 µm.
Afin de facilité la mesure au microscope, la gouttelette ne doit pas être trop rapide.
En déduire s'il est préférable de sélectionner une grosse ou une petite gouttelette.
La
vitesse doit être la plus petite possible. La vitesse est
proportionnelle au carré du rayon de la gouttelette : il faut donc
choisir une petite gouttelette.
Remontée de la gouttelette.
Un
champ électrique uniforme étant établi entre les plaques A et B, la
gouttelette subit une force supplémentaire F verticale et remonte alors
avec une vitesse constante v2 atteinte presque instantanément.
On peut montrer que la charge q de la gouttelette est donnée par la relation : q = -6 p h r ( v1+v2) / E. Plusieurs mesures ont été réalisées pour différentes gouttelettes :
| n° de la gouttelette | r (µm) | v1 ( x 10-4 m/s) | v2 ( x 10-4 m/s) | q (C) | q / e | | 1 | 1,2 | 1,55 | 1,59 | -6,4 10-19 | - 4 | | 2 | 1,3 | 1,82 | 1,81 | -8,0 10-19 | - 5 | | 3 | 1,5 | 2,42 | 1,35 | -9,6 10-19 | - 6 | | 4 | 1,6 | 2,76 | 3,13 | -1,6 10-19 | -1 | | 5 |
| 1,82 | 2,53 | -9,6 10-19 | -6 |
Déterminer sans calcul le rayon de la gouttelette n°5. Justifier. Pourquoi leurs vitesses de remontée sont-elles différentes ?
Les gouttelettes n°2 et n°5 ont la même vitesse de descente. Pour ces deux gouttelettes rg/h est constant. Elles ont donc le même rayon r = 1,3 µm.
Par contre, ne possédant pas la même charge, leurs vitesses de remontée sont différentes.
Montrer que la charge de ces gouttelettes est quantifiées, c'est à dire qu'elle ne prend que des valeurs multiples d'une même charge élémentaire égale à 1,6 10-19 C.
Voir dernière colonne du tableau.
En quoi le protocole de l'expérience effectuée par Milikan diffère-t-il de celui réalisé par Thomson ?
En
1897, Thomson détermine le rapport e / m de l'électron sans pouvoir
trouver la charge et la masse de l'électron. Milikan détermine la
valeur de la charge de l'électron.
|
|
|
Diffraction des électrons.
Davisson
et germer réalisent en 1927 une expérience de diffraction des électrons
sur un cristal constitué d'un arrangement régulier d'atomes de
nickel. De son côté G P Thomson fait une expérience analogue et réussit
également à diffracter un faisceau d'électrons. Il reçoit en 1937 le
prix Nobel de physique pour ses travaux, prix qu'il partagea avec
Davisson.
Quelle information sur la nature de l'électron cette expérience donne-t-elle ?
Dans
l'infiniment petit il faut prendre en compte la dualité onde corpuscule
: dans une expérience de diffraction, l'électron est considéré comme
une onde.
Dans l'expérience de Davison et Germer, les électrons avaient une vitesse égale à 4,4 106 m/s.
Calculer la longueur d'onde de matière associée à un électron ayant cette vitesse.
l = h / (mv) =6,63 10-34 /(9,1 10-31*4,4 106) ~1,7 10-10 m.
Quelle est l'ordre de grandeur de la distance entre les atomes dans un solide. Commenter cette valeur.
La distance entre les atomes dans un solide est de l'ordre de 10-10 m.
On
observe un phénomène de diffraction lorsque la dimension de l'obstacle
( distance entre deux plans réticulaires dans un cristal ) est du même
ordre de grandeur que la longueur d'onde de l'onde.
|
|
|

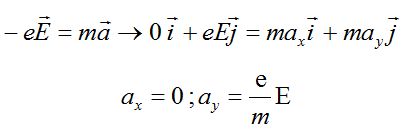

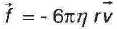 dans laquelle
dans laquelle