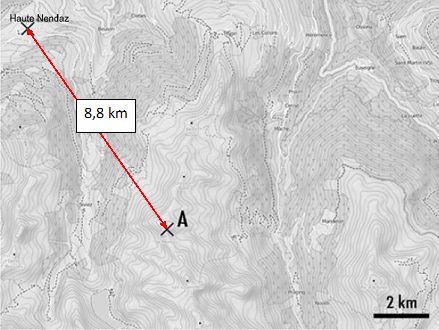
Le cor des Alpes. Bac S  2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Un berger, situé au sommet d’une colline (point A sur la carte) joue la note la plus grave de son cor des Alpes. Son instrument a une longueur de 3,4 m. Pourra-t-on l’entendre à Haute Nendaz si le niveau d’intensité sonore est de L=100 dB à un mètre de l’instrument ? Hypothèses de travail : - L’amortissement de l’onde n’est pas pris en compte : la dissipation d’énergie au cours de la propagation est négligeable. - Le rayonnement de la source est supposé isotrope. Intensité sonore à 1 m de l'instrument :  I = I0 10L/10 =10-12*1010 = 10-2 W m-2. Pour une source isotrope de puissance P, l’intensité sonore I au point M dépend de la distance d à la source et s’exprime de la façon suivante : I = P / (4pd2). Intensité sonore à 8,8 103 m de l'instrument : I' = I / d2 = 0,01 / (8,8 103)2 =1,3 10-10 W m-2. Niveau sonore correspondant : I' = 10 log ( I'/I0) =10 log (1,3 10-10 /10-12)=21 dB. La température de l'air étant voisine de 20°C, la célérité du son dans l'air est c = 343 m/s. Longueur du son émis = 2 fois longueur du cor ; l = 6,8 m. Fréquence du son émis : f = c / l = 343 / 6,8 ~ 50 Hz. . . Le graphique suivant indique les valeurs minimales de niveau d’intensité sonore audible en fonction de la fréquence. 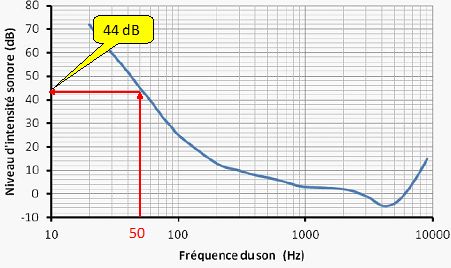Un son de fréquence 50 Hz, de niveau sonore 21 dB, n'est pas audible à une distance de 8,8 km. . . .

menu