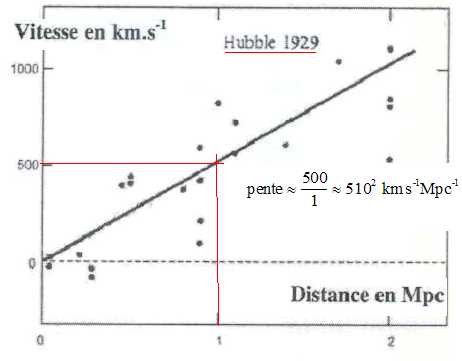
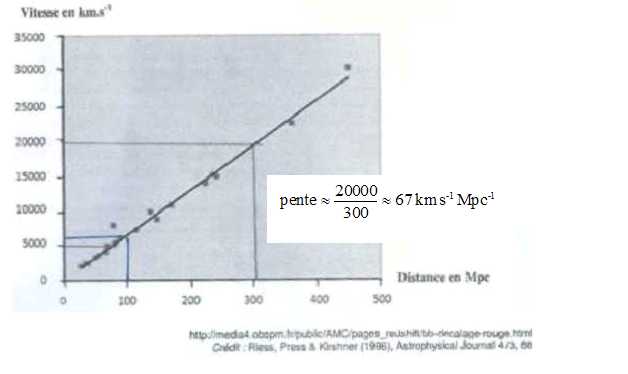
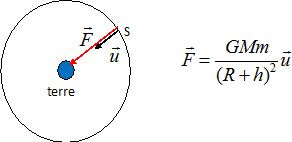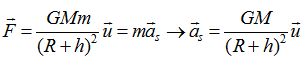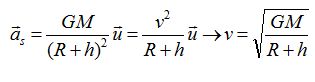Le monde selon Hubble. Bac S Asie 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Le satellite Hubble. Indiquer les limites en longueur d'onde de la partie visible du spectre électromagnétique. 400 nm à 800 nm ou 0,4 µm à 0,8 µm. Justifier l'expression " en infrarouge ou ultraviolet, sans les contraintes dues à l'atmosphère terrestre". 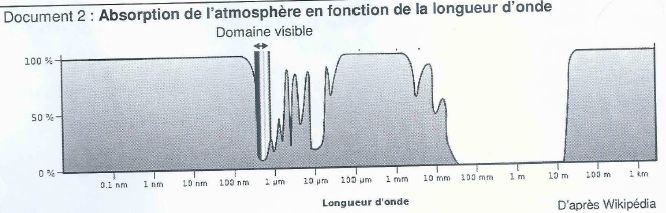L'atmosphère terrestre absorbe pratiquement tout le rayonnement UV et une grande partie du rayonnement IR reçus par la terre. Le télescope Hubble étant placé à 600 km d'altitude, bien au dessus de l'atmosphère terrestre, peut effectuer des observations non seulement dans le domaine visible, mais également dans les domaines UV et IR. Citer une source de rayonnement ultraviolet extraterrestre détectable par le HST. Le soleil, les étoiles, les galaxies. Mouvement du satellite. Représenter sans souci d'échelle la force d'interaction gravitationnelle exercée par la terre sur le satellite. 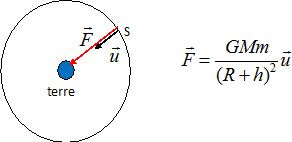On suppose que les durées de parcours du satellite sur sa trajectoire circulaire entre les points H1 et H'1 puis H2 et H'2 sont égales. Enoncer la deuxième loi de Kepler et compléter la figure pour illustrer cette loi. Le mouvement du satellite est tel que le segment de droite reliant le centre de la terre et le satellite balaie des aires égales pendant des durées égales. 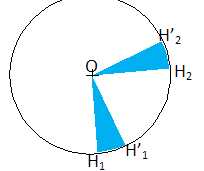En déduire que le mouvement du satellite est uniforme. Longueur de l'arc de cercle H1H'1 = v Dt ;  longueur de l'arc de cercle H2H'2 = v Dt. La norme de la vitesse est donc constante : le mouvement est uniforme. Etablir à l'aide des lois de Newton l'expression de la valeur a de l'accélération du satellite dans le référentiel géocentrique en fonction deG, M, h et R, rayon de la terre. La seconde loi de Newton conduit à : . . 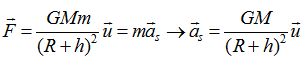Montrer que la vitesse du satellite peut se mettre sous la forme v =(GM / (R+h))½. 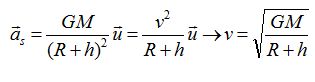Le calcul de la vitesse conduit à v ~7 km/s. Montrer que cette valeur est compatible avec les données. Hubble accomplit le tour de la terre en environ 100 min. Il décrit une circonférence d'environ 42 000 km. v ~42 000 / (100*60) =42 / 6 = 7 km/s. . L'effet Doppler. Indiquer dans le cas d'une source sonore s'éloignant de l'observateur si le son perçu par celui-ci est plus aigu ou plus grave que le son perçu lorsque la source est immobile. Si le corps s'éloigne de l'observateur la fréquence du son perçu diminue et le son est donc plus grave. La galaxie NGC 3627 s'éloigne-t-elle ou se rapproche-t-elle de la terre ? La longueur d'onde de la raie de l'hydrogène de la galaxie est décalée vers le rouge, la galaxie s'éloigne donc de la terre. Commenter la phrase " E. Hubble a remarqué que la vitesse à laquelle semblait s'éloigner les galaxies qu'il observait était proportionnelle à leur distance à la terre". Il s'agit de la première preuve de l'expansion de l'univers. Les galaxies s'éloignent les unes des autres à une vitesse approximativement proportionnelle à leur distance. La constante de proportionnalité est appelée constante de Hubble et noté en général H0. Estimer la valeur de H0 en précisant l'unité. Sur ce graphique, les points sont très dispersés, la valeur obtenue pour H0 ne doit pas être précise. En réalité des mesures plus récentes réalisées en partie par le télescope Hubble ont permis d'obtenir des mesures plus précises sur les galaxies plus éloignées Discuter la validité de la loi de Hubble et comparer la valeur actuelle de H0 à celle proposée par E. Hubble. Cette loi n'est valable que pour de faibles vitesses, c'est à dire pour des distances relativement faibles. Expliquer pourquoi l'application de cette loi pour une galaxie située à 10 000 Mpc se heurterait à un principe fondamental de la physique. Vitesse de cette galaxie : 67 *107 ~6,7 108 m s-1, valeur supérieure à la vitesse de la lumière dans le vide. Aucun corps matériel ne peut dépasser la vitesse de la lumière dans le vide. .

menu