Effet
piézoélectrique. Bac S Afrique 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
La
déformation, sous l’effet d’une action mécanique, de certains cristaux
ou céramiques dits anisotropes, induit l’apparition d’une tension
électrique U ; c’est l’effet piézoélectrique direct, découvert en 1880
par Pierre et Jacques Curie.
Modélisation simplifiée de l’effet piézoélectrique au niveau microscopique.
Un cristal entier est constitué d’un empilement régulier de petits
arrangements qui se répètent dans les trois directions de l’espace.
Considérons au niveau microscopique, un arrangement d’anions et de
cations schématisé ci-dessous, tel qu’il peut en exister dans un
cristal.
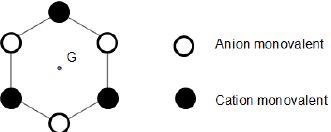
Quand
aucune contrainte mécanique n’agit sur le cristal, pour chaque
arrangement élémentaire, le « centre » des charges électriques
positives coïncide avec celui des charges électriques négatives (point
G sur la figure). En revanche, dès que le cristal est comprimé, cette
coïncidence disparaît, comme le montre le schéma suivant (points G+ pour les charges positives et G–
pour les charges négatives). Cette compression est modélisée par deux
forces opposées de même module F ; la séparation est d’autant plus
importante que la compression est grande.
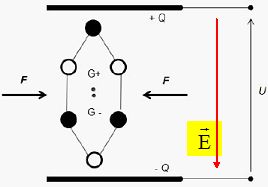
Cette dissymétrie des « centres » de charges électriques pour chaque
arrangement élémentaire conduit à l’apparition de charges électriques
sur les faces extérieures du cristal, générant ainsi un champ
électrique. Une tension électrique U, mesurable, apparaît alors entre
les deux surfaces extérieures du cristal. En pratique, ces surfaces
sont métallisées pour permettre les connexions nécessaires à
l’utilisation du cristal dans un circuit électronique.
Représenter
le champ électrique macroscopique généré par l’apparition des charges
électriques sur les faces extérieures du cristal schématisées sur la
figure.
Le champ électrique pointe vers le plus petit potentiel. ( voir schéma ci-dessus).
Relation
entre l’intensité sonore I, en un point M du milieu de propagation, et
l’amplitude de la pression acoustique p en ce point : I =p2 / (2 ρ c)
Où r désigne la masse volumique du milieu de propagation et c la célérité de l’onde sonore dans ce milieu.
Valeurs de l’intensité sonore de référence I0 et de p0 l’amplitude de la pression acoustique de référence liée à I0.
I0 = 1,0 ×10 - 12 W·m - 2 ; p0 = 2 × 10 - 5 Pa.
Montrer que le niveau d’intensité sonore L et la pression p sont reliés par la relation : L = 20 log ( p / p0).
I / I0 = (p / p0)2.
L = 10 log ( I / I0) =10 log (p / p0)2 = 20 log (p / p0).
|
| .
. |
|
|
Caractéristiques du fonctionnement d’un capteur piézoélectrique au niveau macroscopique.
Le capteur a un comportement un peu différent du cristal décrit en introduction.

En
effet, les charges électriques apparaissent sur les faces soumises à
l’action mécanique modélisée par les deux forces opposées de module F ;
une charge électrique +Q (Q > 0) apparaît sur la face supérieure
tandis qu’une charge –Q apparaît sur l’autre face. Le module F de la
force et la charge Q sont proportionnels ; le coefficient de
proportionnalité ß est appelé constante piézoélectrique.
β = 5 × 10 -5 C · N -1 pour le capteur de la figure.
La charge Q est également proportionnelle à la tension électrique U qui
apparaît entre les deux faces : Q = CU où la charge Q est exprimée en
coulomb et la tension électrique U en volt. C = 125 × 10-12 F (farad) pour le capteur.
|
.
|
|
On connecte le capteur piézoélectrique aux bornes d’un voltmètre.
Évaluer
l’ordre de grandeur de la tension électrique U affichée par le
voltmètre quand le capteur piézoélectrique est soumis à un son
d’intensité sonore L = 50 dB, placé à 50 cm d’une source sonore ? Peut-on prévoir d’utiliser ce capteur pour réaliser un sonomètre ?
p = p0 10L/20 = 2,0 10-5 *102,5 =6,32 10-3 Pa.
Le diamètre du capteur est de l'ordre du centimètre ; sa section est de l'ordre de S= pd2/4 = 3,14 *10-4/4 =8 10-5 m2.
Force pressante F = p S =6,32 10-3 *8 10-5 ~5 10-7 N.
Or ß = Q/F et Q = CU d'où : U =ß F/C =5 10-5 *5 10-7 / (125 10-12)=0,2 V.
Un calcul identique pour des niveaux sonores L = 30 dB et L = 120 dB conduit respectivement à : 0,02 V et 640 V.
L'amplitude de tension est trop grande.
Pour utiliser ce capteur dans un sonomètre, il faudra prévoir deux
gammes de mesures : l'un allant par exemple de 20 à 60 dB et l'autre de
60 à 120 dB.
Pour la première gamme il faudra amplifier la tension et pour la seconde, il faudra la diminuer par un montage électronique.
|
|
|


