Détermination
expérimentale d'une résistance thermique. Bac S Afrique 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Pour
déterminer expérimentalement la résistance thermique du verre, il est
possible de mettre en oeuvre le protocole schématisé ci-dessous.
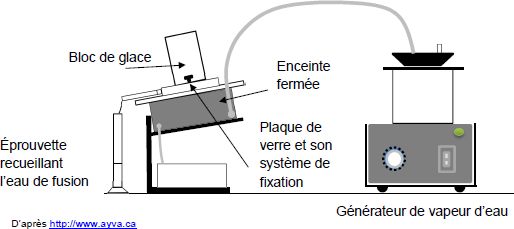
On place, sur une enceinte fermée pouvant recevoir un courant de vapeur
d’eau, une plaque de verre carrée de 12 cm de côté, et sur celle-ci un
bloc de glace cylindrique de diamètre d = 8 cm. Le transfert thermique
à travers la plaque de verre, soumise à un écart de température Dq
permet la fusion du bloc de glace plus rapidement qu’en le laissant à
la température du laboratoire. La plaque de verre utilisée a une
épaisseur e = 4 mm.
L’objectif de cet exercice est de montrer comment ce dispositif permet
d’évaluer la valeur de la résistance thermique d’un matériau. Chaleur
massique de fusion de la glace Lf = 333,5 J g-1.
Pour atteindre l’objectif fixé, il est nécessaire de procéder à deux
expériences.
Première
expérience :
on laisse fondre un bloc de glace pendant une durée Δt = 5 min 30 s, à
la température ambiante du laboratoire. Au bout de cette durée, on
recueille une masse d’eau liquide m1 = 5,5 g. Le diamètre d
du bloc de glace conserve pratiquement son diamètre initial (d = 7,8 cm
à la fin de l’expérience).
Seconde expérience
: le bloc de glace est placé sur le même support, pendant la même durée
Δt = 5 min 30 s, mais cette fois le générateur de vapeur d’eau est mis
en fonctionnement. La masse de glace fondue est alors m2 =
124,4 g. La mesure du diamètre du bloc de glace est proche de celle
obtenue lors de la première expérience : d = 7,6 cm à la fin de
l’expérience).
Remarque :
la masse de glace fondue est mesurée grâce à la masse d’eau recueillie
dans l’éprouvette.
Montrer que la
valeur de l’énergie thermique Eth
transférée à travers la paroi de verre et due à la mise en route du
générateur de vapeur au cours de la deuxième expérience, est de l’ordre
de 40 kJ. Préciser le mode de ce transfert thermique mis en oeuvre et
proposer uneinterprétation au niveau microscopique. .
Le
transfert thermique s'effectue par conduction à travers la paroi de
verre par contact entre un corps chaud et un corps froid. Au niveau
microscopique, on l'interprète comme la transmission de proche en
proche de l'agitation thermique : un atome, une molécule cède une
partie de son énergie cinétique au plus proche voisin.
Eth = Lf(m2-m1)=333,5(124,4-5,5)=3,96
104 J ~40 kJ.
|
| .
. |
|
|
On appelle
flux thermique moyen à travers une paroi plane, la grandeur Φ définie
par la relation :
Φ =Eth / Δt
Exprimer
l’unité du flux thermique Φ en fonction des unités du système
international (mètre, kilogramme et seconde). Avec quelle unité
exprime-t-on généralement, plus usuellement, le flux thermique ?
Eth s'exprime en joule c'est à dire une force fois un
déplacement ; une force est une masse fois une accélération.
[Eth]= M L2T-2 ; [Φ]=M L2T-3
; l'unité usuelle est le watt.
Calculer la valeur
du flux thermique à travers la plaque de verre étudiée.
F = 40 103
/ (5*60+30) =1,2 102 W .
La résistance thermique Rth de la portion de verre comprise
entre le bloc de glace et l’enceinte fermée est reliée au flux
thermique moyen Φ à travers la plaque de verre, par la relation :
Φ =Δθ / Rth où Δθ représente l’écart de température
entre les deux faces de la plaque de verre.
Déterminer
la résistance thermique du verre.
Rth = Δθ /
Φ =(100-0) / (1,2 102) =0,83 K W-1.
|
.
|
|
La mesure de la
résistance thermique du verre est réalisée 12 fois, dans les mêmes
conditions expérimentales. Les valeurs obtenues, exprimées avec l’unité
du système
international, sont rassemblées dans le tableau suivant :
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
Rth
|
0,81
|
0,89
|
0,78
|
0,82
|
0,87
|
0,78
|
0,76
|
0,92
|
0,85
|
0,84
|
0,81
|
0,79
|
| (Rth-Rth
moy)2 |
2,89
10-4 |
3,97
10-3 |
2,21
10-3 |
4,9
10-5 |
1,85
10-3 |
2,21
10-3 |
4,49
10-3 |
8,65
10-3 |
5,29
10-4 |
1,69
10-4 |
2,89
10-4 |
1,37
10-3 |
Somme (Rth-Rth
moy)2= 2,6 10-2.
Soient
Rth moy la moyenne des n mesures réalisées et U( Rth
) l’incertitude de mesure correspondante, associée au niveau de
confiance de 95%.
Par définition : U( Rth )=t95 sn-1 / n½. 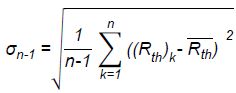
t95 est appelé coefficient de Student. Pour n = 12 mesures
et pour le niveau de confiance choisi de 95%, t95= 2,20.
Écrire le résultat
de la mesure expérimentale de Rth correspondant à un niveau
de confiance de 95%.
Rédiger une phrase de conclusion traduisant la signification du
résultat de la mesure de Rth donnée par la relation
précédente.
Rth moy =0,827~0,83 ; sn-1
= 4,87 10-2. U( Rth )=2,20*4,87 10-2 / 12½ =3,1 10-2.
Rth =Rth moy ±U( Rth )=0,83 ±0,03 K W-1.
Au niveau de confiance de 95 %, la résistance thermique du verre est
comprise entre 0,80 et 0,86 K W-1.
Dans l’industrie du bâtiment, les matériaux ne
sont pas caractérisés par leur résistance thermique Rth mais
plutôt par leur résistance thermique surfacique R (ou résistance
thermique par unité de surface). Déterminer la valeur
de R du verre utilisé dans le dispositif expérimental.
Section de la glace : p d2/4 = 3,14 *(7,8 10-2)2/4=4,78
10-3 m2 ; R =0,83* (4,78 10-3)~4,0 10-3 W K-1m2.
Le constructeur indique une valeur plus élevée que celle obtenue
expérimentalement.
Proposer
une interprétation pour expliquer cette différence.
Le diamètre du bloc de glace n'est pas constant au cours de
l'expérience.
|
|
|