Fibre optique à
saut d'indice,
concours orthoptie Montpellier 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
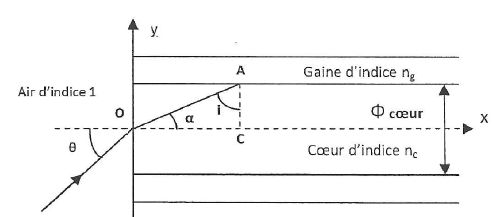
Une fibre optique à saut d'indice est formée d'un coeur cylindrique en verre de diamètre Fcoeur = 50 µm, d'axe Ox et d'indice nc=1,54, entouré d'une gaine optique d'indice ng = 1,52. Un rayon situé dans le plan Oxy entre dans la fibre au point O avec un angle d'incidence q.
A quelle condition sur i, angle d'incidence à l'interface coeur/gaine, le rayon reste-t-il confiné à l'intérieur du coeur ? Donner la valeur de cet angle limite noté iL.
Loi de Descartes concernant la réfraction en A : ncoeur sin i = ng sin r.
sin r = ncoeur /ng sin i avec sin r inférieur ou égal à 1.
or ncoeur /ng >1, il existe donc un angle limite iL au dela duquel l'angle r n'existe pas ( absence de réfraction en A, mais réflexion totale ).
Il y a réflexion totale en A ( le rayon reste dans la gaine) si : 1 = ncoeur /ng sin iL ;
sin iL = ng/ ncoeur= 1,52 / 1,54 = 0,987 soit iL =80,76 ~80,8°.
Dessiner le trajet ultérieur du rayon en faisant apparaître plusieurs réflexions.
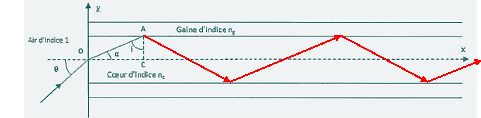
Montrer que la condition précédente est vérifiée si q est inférieur à un angle limite qL tel que :
Les angles a et iL ssont complémentaires : sin a = cos iL.
Réfraction en O : nair sin qL =nc sin a = nc cos iL. De plus nair = 1.
|
|
|
En déduire l'ouverture numérique ON de la fibre définie par ON =sin qL en fonction de nc et ng uniquement.
ON =sin qL =nc cos iL.
sin qL=nc cos iL. De plus sin iL = ng/ nc.
cos2iL = 1-sin2iL =1-(ng/ nc)2.
ON = nc[1-(ng/ nc)2]½ = [nc2-ng2]½.
Calculer cette ouverture numérique.
ON=(1,542-1,522)½=0,0612.
Un rayon entre dans la fibre en O avec un angle d'incidence limite qL.
Calculer la distance OA.
OA = AC / sin a. AC = 25 µm = 25 10-6 m.
Les angles a et iL ssont complémentaires : a = 90 -80,8 = 9,2°.
OA = 25 10-6 /sin 9,2 = 1,5637 10-4 ~1,56 10-4 m.
|
.
|
|
Calculer la distance OC puis le rapport OA / OC.
OC = OA cos a = 1,5637 10-4 cos 9,2 =1,5435 10-4 ~1,54 10-4 m.
OA / OC=1,5637 / 1,5435 =1,01309 ~1,013.
En déduire la distance parcourue par le rayon dans la fibre si celle-ci fait 1 km de long.
OA = 1,013 OC =1,013 km.
Exprimer la vitesse de propagation de la lumière dans le coeur de la fibre.
v = c / nc = 3,00 108 / 1,54 = 1,948 108 ~1,95 108 m/s.
Calculer la différence de temps Dt entre ce rayon et un rayon qui parcourrait l'axe Ox dans la fibre.
La différence de distances est de 13,09 m par km de fibre.
Dt = 13,09 /(1,948 108) =6,72 10-8 s.
Déterminer la fréquence maximale de répétition pour que les impulsions ne se recouvrent pas en bout de fibre.
L'impulsion n°2 doit attendre que l'impulsion n°1 ayant emprunté le parcours le plus long OA soit arrivée en bout de fibre.
La durée séparant deux impulsions consécutives est donc 6,72 10-8 s.
Fréquence maximale de répétition : 1/(6,72 10-8) =1,49 107 Hz.
|
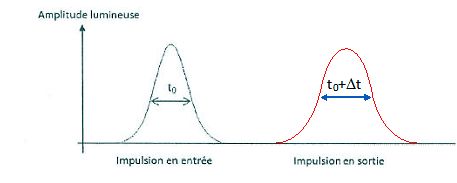
On injecte à l'entrée de la fibre une impulsion lumineuse de durée t0 formée par un faisceau de rayons ayant un angle d'incidence compris entre 0 et qL. La figure suivante représente l'allure du signal lumineux en fonction du temps.
Représenter l'allure du signal lumineux à la sortie de la fibre. Quelle durée a approximativement l'impulsion lumineuse en sortie de fibre ?
Le signal emprunte tous les chemins possibles entre l'axe et le segment OA et son symétrique par rapport à l'axe Ox.
La durée approximative du signal de sortie sera donc t0 +Dt.
|
|