QCM de physique, concours Ergothérapie Berck 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . On donne g = 10 m s-2 ; 10½ = 3,2 ; 2p~6,3. Marégraphe à ultrasons. Le schéma suivant représente le principe d'un marégraphe à ultrasons. Pour mesurer la hauteur de la marée, un télémètre émet un bref signal ultrasonore qui se réfléchit à la surface de l'eau. On note Dt la durée entre l'émission et la réception du signal. Célérité des ultrasons dans l'air v = 340 m/s ; H = 15,0 m ; Dt = 50,0 ms. Le schéma n'est pas à l'échelle. 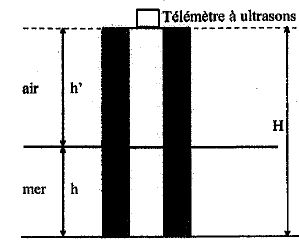Calculer la hauteur h de la marée ( en mètre ).6,5 ; 7,0 ; 7,5 ; 8,0 ; 8,5 ; aucune réponse exacte. 2h' = v Dt ; h' = ½v Dt =0,5*340*0,0500 =8,5 m ; h = H-h' = 15-8,5 = 6,5 m. Diffraction par une fente. 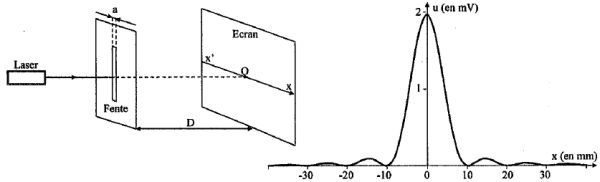La lumière d'un laser de longueur d'onde l est diffractée par une fente fine verticale de largeur a. On observe la figure de diffraction sur un écran situé à la distance D de la fente. On déplace une cellule photoélectrique le long de l'axe horizontal x'x. L'origine O des abscisse correspond au centre de la figure de diffraction sur l'écran. La position de la cellule est repérée par l'abscisse x. Cette cellule délivre une tension u proportionnelle à l'intensité lumineuse. On obtient la courbe ci-dessus représentant la tension u en fonction de l'abscisse x. On donne D = 2,00 m et a = 100 µm.  Calculer l ( en nm). 450 ; 500 ; 550 ; 600 ; 650 ; aucune réponse exacte. 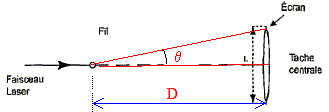tan q = ½L/D voisin de q radian pour les angles petits. d'autre part q = l/a. avec : l longueur d'onde (m) et a : largeur de la fente (m). en tenant compte des deux relations ci-dessus : ½L/D=l/a soit a=2lD/L ou l = aL / (2D). D'après la figure,la largeur de la bande centrale vaut L = 20 mm. l =100 10-6 *20 10-3 / (2*2,00) =5,00 10-7 m = 500 nm. . La houle. La houle peut être modèlisée par une onde mécanique périodique, sinusoïdale, se propageant à la surface de la mer. En haute mer, la longueur d'onde l de la houle est petite devant la profondeur de la mer. Dans ce cas, on peut calculer la célérité v de la houle par v = (kl/(2p))½ où k est une constante.    Par analyse dimensionnelle, déterminer l'unité de k. m s-1 ; N kg-1 ; Nm-1 ; m2s-1 ; N s-1 ; aucune unité exacte. 2 p est sans dimension, la célérité s'exprime en ms-1 et l s'exprime en m. k =2pv2 / l. k s'exprime en m2 s-2 m-1 soit en m s-2. Durée de freinage. Sur une patinoire horizontale, un palet de hockey est animé d'un mouvement rectiligne uniformément décéléré. Le palet dont la vitesse initiale est v0 = 54 km/h s'immobilise après avoir parcouru une distance L = 30 m. Calculer la durée ( en s) du freinage du palet. 2,0 ; 2,5 ; 3,0 ; 3,5 ; 4,0 ; aucune réponse exacte. Le palet est soumis à son poids, à l'action du plan opposée au poids et à une force de freinage supposée constante, parallèle au plan, de sens contraire au mouvement. Le théorème de l'énergie cinétique conduit à : 0-½mv02 = -f L ; f = ½mv02 / L. La seconde loi de Newton donne l'accélération  a = -f/m = -½v02 / L avc v0 = 54/3,6 = 15 m/s.  a = -0,5*152 / 30 = -3,75 m s-2. La vitesse est une primitive de l'accélération v = -3,75 t + v0. A l'arrêt v=0 soit t = v0 / 3,75 = 15 / 3,75 =4,0 s. Joueur de tennis. 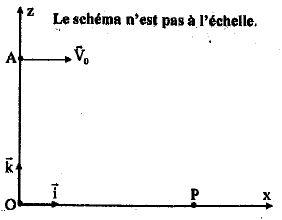Pour effectuer un service, un joueur de tennis lance une balle verticalement vers le haut, d'un point situé à 1,60 m au dessus du sol. Il frappe la balle avec la raquette lorsqu'elle atteint le sommet A de sa trajectoire, situé 0,40 m plus haut. La balle part alors avec une vitesse horizontale v0. La balle touche le sol en un point noté P. La balle sera considérée comme ponctuelle et on étudiera sa trajectoire dans le plan ( O, i, k ). L'origine O du repère se trouve au niveau du sol. On néglige l'action de l'air sur la balle. On donne v0 = 35 m/s. Calculer l'abscisse ( en m ) du point P.14 ; 16 ; 18 ; 20 ; 22 ; aucune réponse exacte. Mouvement de chute libre : les composantes de l'accélération sont : ax=0 et az = -g. La vitesse est une primitive de l'accélération : vx = v0 ; vz = -gt. La position est une primitive de la vitesse : x = v0t ; z = -½gt2+ OA. Trajectoire : z = -½g(x/v0)2 + OA ; z = -5x2/352 +2,00. En P, z=0 : 5x2/352 =2,00 ; x2 = 352*2/5 =4/ 10 *352 ; x = 35*2/3,2 =70/3,2 ~ 22 m. Satellite. Un satellite décrit une orbite circulaire autour de la terre. Le satellite se situe à l'altitude h par rapport à la surface de la terre et sa période de révolution est notée T. Rayon terrestre R = 6370 km ; h = 290 km ; T = 1 h 30 min ; G = 6,67 10-11 SI. Calculer ( en km/h) la valeur de la vitesse du satellite sur son orbite. 1,6 104 ; 2,0 104 ; 2,4 104 ; 2,8 104 ; 3,2 104 ; aucune réponse exacte. Le satellite décrit la circonférence 2p(R+h) en T seconde à la vitesse v constante. v = 2p(R+h) / T =2*3,14(6370+290)/1,5 = 6,3*6660 /1,5 =2,8 104 km/h. 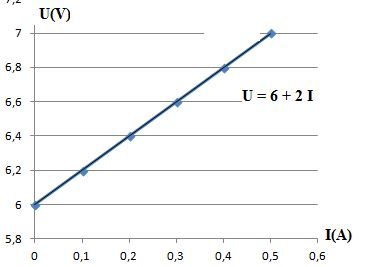Moteur électrique. On a relevé expérimentalement la tension UAB aux bornes d'un moteur traversé par un courant d'intensité I. UAB (V) 6,0 6,2 6,4 6,6 6,8 7,0 I(mA) 0 100 200 300 400 500 UAB = E' + r'I avec E' tension à vide du moteur et r' sa résistance interne. Calculer la valeur de sa résistance interne ( en ohm).2,0 ; 4,0 ; 6,0 ; 8,0 ; 10,0 ; aucune réponse exacte. E' = 6,0 V, tension à vide. r' = 2 ohms. L'atome d'hydrogène. Rutherford a décrit l'atome d'hydrogène suivant le modèle planétaire : l'électron E de masse me et de charge -e est en mouvement circulaire uniforme autour du noyau constitué uniquement d'un proton P de masse mP et de charge +e. La distance entre l'électron et le proton est notée r. L'électron n'est soumis qu'à la force électrostatique Fe exercée par le proton. On propose différentes expressions pour la vitesse v de l'électron. Certaines de ces expressions ne sont pas possibles. Parmi les expressions proposées, laquelle est exacte ?   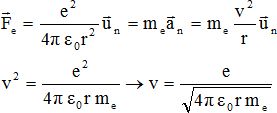La proposition d est exacte. la

menu