Réussir son panier au basket, Concours Audioprothésiste Rennes 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . On étudie la trajectoire du centre d'inertie d'un ballon de basket-ball vers le cercle du panier de l'équipe adverse par un joueur attaquant. On ne tient pas compte de la résistance de l'air ni de la rotation éventuelle du ballon. Le lancer est effectué vers le haut ; on lâche le ballon lorsque son centre d'inertie est en A. Sa vitesse initiale est représentée par le vacteur v0 situé dans le plan ( O, i, j) et faisant un angle a avec l'axe horizontal. g = 9,8 m s-2 ; a = 40° ; diamètre du ballon 25 cm. 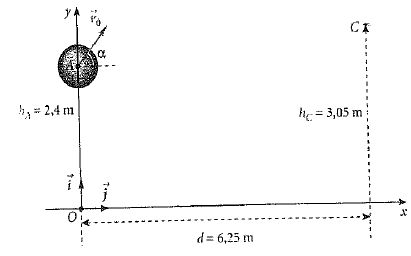Pour t=0, indiquer les valeurs litérales ou numériques des vecteurs position et vitesse. x0 = 0 ; y0 = hA = 2,4 m ; v0x = v0 cos a = v0 cos 40 = 0,766 v0. v0y = v0 sin a = v0 sin 40 = 0,643 v0. Déterminer les coordonnées du centre d'inertie du ballon. Le ballon n'est soumis qu'à son poids ; la seconde loi de Newton conduit à : ax = 0 et ay = -g. Etablir les expressions littérales des coordonnées du vecteur vitesse et du vecteur position à une date t. Le vecteur vitesse est une primitive du vecteur accélération : vx = constante = v0 cos a ; vy = -gt + constante. La constante d'intégration est déterminée par la vitesse initiale : vy = -gt + v0y =-gt + v0 sin a. Le vecteur position est une primitive du vecteur vitesse. x = v0 cos a t + x0 = v0 cos a t. (1) y = -½gt2 + v0 sin a t + y0 = -½gt2 + v0 sin a t + hA. (2) Montrer que l'expression numérique de la trajectoire dans le repère (O, i, j) s'écrit : y = -8,36 x2/v02 +0,84 x + 2,4. (1) donne t = x /( v0 cos a ) ; repport dans (2) : y = -½g x2 /( v0 cos a )2 + v0 sin a  x /( v0 cos a ) +hA. y = -½*9,8 x2 /( v0 cos 40 )2 + x tan 40  +2,4. y = -8,35 x2 / v02 + 0,84 x +2,4. .  En utilisant les valeurs numériques du schéma, déterminer  la vitesse initiale v0 pour que son centre d'inertie passe exactement au centre C du panier. xC = d = 6,25 m ; yC =hC = 3,05 m. Repport dans l'expression de la trajectoire : 3,05 = -8,36 *6,252 / v02 + 0,84 *6,25 + 2,4. 3,05 = -326,56 / v02 +7,65. 326,56 / v02 = 7,65-3,05 = 4,6. v02 =326,56 / 4,6 = 70,99 ; v0 =8,4256 ~ 8,43 m/s. Quelle serait alors la durée du trajet du ballon du point A au point C ? xC = v0 cos a t ;  t = xC /( v0 cos a ) = 6,25 / (8,4256*cos 40) =0,9683 ~0,968 s. Calculer la vitesse du ballon à son passage en C. vxC = v0 cos a =8,4256 *cos 40 = 6,454 m/s. vyC =-gt + v0 sin a = -9,8*0,9683 +8,4256*sin40 =-9,489 +5,416 = -4,073 m/s. vC = ( 6,4542+(-4,073)2 ) ½ =7,63 m/s. Autre méthode : conservation de l'énergie mécanique entre A et C. ½mv02 + mghA = ½mvC2 + mghC. v02 + 2ghA = vC2 + 2ghC. vC2  = v02 + 2g(hA-hC). vC2  =70,99 +2*9,8(2,4-3,05) =58,25 ; vC =7,63 m/s. .

menu