Au sujet des ondes : célérité, acoustique musicale, diffraction, Concours Audioprothésiste Rennes 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Célérité dans la fonte. Sur un conduit de fonte contenant de l'eau, on place un capteur de pression. Un coup est donné dur le conduit à une distance d du capteur. On détecte deux signaux, séparés par un intervalle de temps Dt = 0,46 s. Que vaut la distance d ? 690 m ; 986 m ; 1610 m ; 2300 m. Célérité du son dans l'eau : c1 = 1500 m/s ; dans la fonte : c2 = 5000 m/s. d = c1 t1 ; d = c2 t2 avec t1-t2 = Dt. t1 = d/c1 ; t2 = d/c2 ; d(1/c1 -1/c2) = Dt. d (1/1500 -1/5000 ) = 0,46 ; d =986 m. Onde sur une corde. 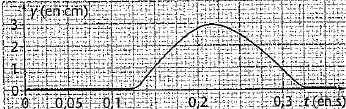On filme la propagation d'une onde le long d'une corde sur un axe x. Par traitement informatique, on a obtenu le graphe suivant donnant, en fonction du temps, l'évolution de la position d'un point M de la corde situé à 40 cm de la source S. t0 = 0 est l'instant où la perturbation a commencé à être émise en S. Quelle est la célérité de la perturbation ? 0,14 m/s ; 1,23 m/s ; 1,8 m/s ; 3,2 m/s. La perturbation atteint le poiunt M, situé à 0,40 m de S, au bout de 0,125 s : c = 0,40 / 0,125 = 3,2 m/s. Célérité des ondes sur un fil. A 25°C, v = 1000 m/s. On réalise le montage suivant afin de mesurer la calérité des ondes sur le fil du dispositif. 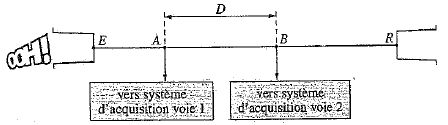Deux capteurs, reliés en deux points A et B distants de D = 20 m sur le fil du pot de yaourt émetteur E. Les capteurs enregistre l'amplitude de cette perturbation au cours du temps. A partir de l'enregistrement, déterminer avec que retard t, par rapport au point A, le point B est atteint par le signal. t = D / v = 20 / 1000 = 0,020 s = 20 ms. Quelle est la sensibilité horizontale ? 1 ms/div ; 4 ms / div ; 5 ms/div ; 10 ms/div. 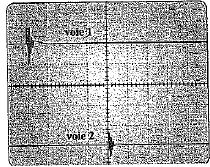Le signal voie 2 est en retard de 20 ms par rapport au signal voie 1 ; cela correspond à 4 divisions sur l'écran. La sensibilité horizontale est donc : 20 / 4 = 5 ms/div. . Acoustique musicale. On enregistre à l'aide d'un microphone, quatre notes produites par des instruments quelconques. On observe sur l'écran d'un ordinateur les oscillogrammes suivants ( 0,25 ms/div et 0,1 V / div ). La hauteur d'une note est associée à la fréquence du son émis. Plus un son est grave, plus sa fréquence est basse, c'est l'inverse pour un son aigu. 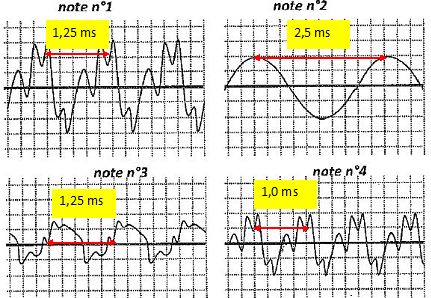Le(s) son(s) le(s) plus aigu(s) est(sont ) : note 1 ; note 2 ; notes 1 et 2 ; note 4. La fréquence en hertz est l'inverse de la période exprimée en seconde : f1 = f3 = 1000 / 1,25 = 800 Hz ; f2 = 1000 / 2,5 = 400 Hz ; f4 = 1000 Hz. La note 4 possède la fréquence la plus élevée, elle correspond au son le plus aigu. Laser et diffraction. On utilise un pointyeur laser dans le montage suivant : une fente verticale de largeur a très petite, est placée sur le trajet du faisceau et un écran est placé à la distance D de la fente. La lumière issue du laser est diffractée. La figure de diffraction est observée sur un écran placé à la distance D de la fente. La largeur de la tache centrale est notée L. 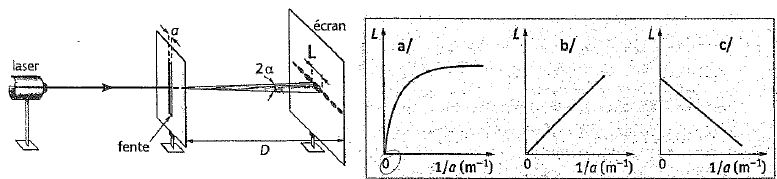On note 2a l'écart angulaire entre les deux premières extinctions entourant la tache centrale. On réalise plusieurs mesures de L pour différentes largeurs de la fente a. Etablir l'expression de L en fonction de a et choisir la bonne représentation graphique. 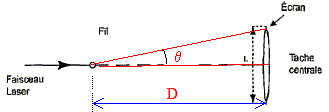tan q = ½L/D voisin de q radian pour les angles petits. d'autre part q = l/a. avec : l longueur d'onde (m) et a : largeur de la fente (m). en tenant compte des deux relations ci-dessus : ½L/D=l/a soit a=2lD/L ou L = 2l D/a. La largeur de la tache centrale est proportionnelle à 1/a. Graphe b.

menu