|
|
|
|
Lu dans le
quotidien Ouest France. le lundi 15 octobre 2012.
Tout s'est déroulé comme prévu pour l'autrichien Félix Baumgartner. Au
terme d'environ 2 h 30 min d'ascension dans une sonde accrochée à un
ballon stratosphérique, il a sauté en chute libre de 39045 m d'altitude
. Après avoir atteint une vitesse maximale de 1342 km/h ( soit
1,24 fois la vitesse du son ) il a déclenché son parachute et s'est
posé sans encombre, signant un authentique exploit.
L'expérimenté parachutiste de 43 ans s'est trouvé en chute libre
pendant 4 min et 20 s avant l'ouverture de son parachute, a
déclaré Brian Utley qui a procédé à l'enregistrement du record pour Red
Bull Stratos.
1342,8 km/h : vitesse maximale franchie au bout de 45 s de chute libre.
1224 km/h : mur du son franchi à z = 29 000 m.
2516 m : altitude au moment de l'ouverture du parachute au bout de 4
min 20 s de chute libre.
Durée du saut : 9 min 30 s.
Document 1
: définition de la chute libre.
Un chute libre est un mouvement accéléré sous le seul effet de la
pesanteur terrestre ( g = 9,81 m s-2). On distingue la simple chute
dans un champ de pesanteur uniforme au voisinage de la terre (
Galilée 1605 ) et la chute céleste ( lois de Kepler ), dont Sir Isaac
Newton fera la synthèse en 1687. Il est convenu que les autres forces
agissant sur le corps, en particulier la résistance de l'air, sont
négligées. Source http : // www.techno-sciences.net.
Document 2.
Nombre de Mach.
Le nombre de Mach est le rapport entre la vitessse de l'avion ( v ) et
la célérité ( c) du son dans l'air. M = v / c. La célérité du son
dans l'air dépend de la température ; M = 1 correspond à 1235 km/h pour
un avion volant à basse altitude par une température de 20 °C, et à
1055 km/h pour une altitude de 10 000 m, et -60 °C.
En dessous de M = 0,8 la vitesse est dite infrasonique ou subsonique ;
pour 0,8 < M < 1,2 elle est transonique, pour 1,2 < M < 5,
elle est dite supersonique et au delà elle est hypersonique.
Source : http ://www.larouse.fr /encyclopedie/divers/mur/72129.
Document 3.
La force de frottement f est proportionnelle, entre autres, à la
pression de l'air.
Altitude
(m)
|
Pression
( hPa)
|
température
(°C)
|
0
|
1013
|
15
|
5000
|
541
|
-17
|
10000
|
265
|
-50
|
15000
|
119
|
-56
|
20000
|
55
|
-46
|
25000
|
26
|
-42
|
30000
|
11
|
-38
|
35000
|
6
|
-20
|
40000
|
1
|
-5
|
|
.
|
A
partir des documents répondre par une argumentation claire et cohérente
aux questions suivantes.
Etablir
les équations horaires en chute libre, représentant l'accélération az,
la vitesse vz et la position z au cours du temps.
Le solide n'est soumis qu'à son poids, verticale vers le bas, valeur
mg. La seconde loi de Newton conduit à az = -g.
La vitesse est une primitive de l'accélération. La vitesse initiale
étant nulle, la constante d'intégration est nulle. vz = -gt.
La position est une primitive de la vitesse. La constante d'intégration
est égale à h, altitude initiale. z = -½gt2 +h.
Montrer que F
Baumgartner, supposé en chute libre, a déja atteint la vitesse de 1224
km/h à une autre altitude.
1224 / 3,6 = 340 m/s ; t = 340 / 9,81 = 34,66 s ; z = -0,5*9,81*34,662
+3,9045 103= 33 153 m ~33,2 km.
Est-il encore en
chute libre lorsqu'il atteint sa vitesse maximale évoquée dans le texte
?
Dans l'hypothèse d'une chute libre, au bout de 45 s de chute la vitesse
atteinte serait : 9,81*45 =441,15 m/s ou 441,15*3.6 =1589 ~1,6 103
km/h.
Or la vitesse maximale n'est que de 1342,8 km/h. F Baumgartner n'est
donc plus en chute libre, les forces de frottement ne sont pas
négligeables.
Pour
sa vitesse maximale atteinte, quel nombre de Mach a-t-il réellement
atteint ?
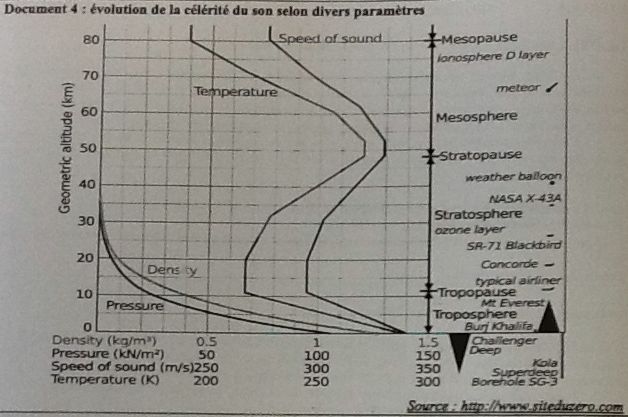
Le document 4 donne une vitesse du son de 300
m/s ( 300*3,6 =1080 km/h) à une altitude de 30 km et 295 m/s ( 1062
km/h) ) à une altitude de 20 km.
1342/1080 = 1,24 ~1,2 Mach ; 1342/1062 = 1,26 ~1,3 Mach.
Montrer
par une approche qualitative et quantitative que F Baumgartner ne peut
pas être en chute libre durant 4 min 20 s.
Dans l'hypothèse d'une chute libre durant 260 s, la vitesse maximale
atteinte serait : 9,81*260 =2550 m/s ( 9,1 103 km/h). La
vitesse réelle atteinte étant très inférieure à cette valeur,
l'hypothèse d'une chute libre durant 4 min 20 s est fausse.
A 2500 m d'altitude, au moment de l'ouverture du parachute,
l'atmosphère est suffisamment dense pour que la résistance de l'air ne
soit plus négligeable devant le poids.
|
|
Montrer
quantitativement qu'entre les dates t = 45 s et t = 4 min 20 s, F
Baumgartner n'a pas pu conserver sa vitesse maximale atteinte. Apporter deux
raisons qualitatives à cette situation.
Dans l'hypothèse d'une chute libre, le
mouvement est uniformément accéléré et la valeur de la vitesse croît de
: 9,81*45 =441,5 m/s à 2550 m/s.
Dans l'hypothèse d'une force de frottement constante, le mouvement est
rectiligne uniforme ( vitesse maximale constante ). Or la force de
frottement est proportionnelle à la pression de l'air et à la vitesse :
la force de frottement croît, le mouvement est alors décéléré.
En
supposant que les forces se compensent suite à l'ouverture du arachute,
déterminer
la valeur de la vitesse moyenne avant son atterrissage au sol.
2516 m : altitude au moment de l'ouverture du
parachute au bout de 4 min 20 s de chute libre. Durée du saut : 9 min
30 s.
Durée de la chute, parachute ouvert : 9 min 30 -4 min 20 = (570 -260) s
= 310 s.
Vitesse moyenne = 2516 / 310 =8,116 m/s = 8,116 *3,6 = 29,2 km/h.
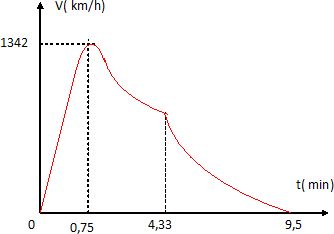
Par
une approche qualitative, vous réalisez un graphe représentant
l'évolution de la valeur de la vitesse de chute de Baumgartner.
Faire apparaître les valeurs de certaines grandeurs temporelles et de
vitesses particulières qui vous semblent essentielles.
|
|