|
|
|
|
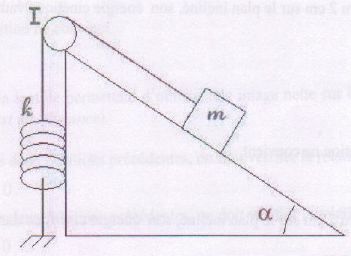
La raideur du ressort est notée k. Le ressort est relié à un bloc de
masse m par un fil ( par l'intermédiaire d'une poulie en I qui ne
jouera aucun rôle par la suite ). le dispositif est initialement au
repos, le ressort est détendu. On néglige les frottements. On ne
s'interesse qu'à la première descente du bloc ( on n'étudie pas les
oscillations et montées suivantes ).
Question
1.
La distance maximale parcourue par le bloc après avoir lâché le système
s'écrit :
A) d = mg cos a
/ k. Faux.
Conservation
de l'énergie
mécanique : l'origine de l'énergie potentielle est la position initiale.
0 = ½k x2 -mgdsin a
avec x =d ; ½k d = mgsin
a
; d
= 2 mg sin a / k.
B) d = mg sin a
/ k. Faux.
C) d = 3mg cos a
/ k. Faux.
D) d = 3mg sin a
/ k. Faux.
E) d = 2mg sin a / k. Vrai.
F) Aucune proposition ne convient. Faux.
Question 2.
La distance maximale parcourue par le bloc après avoir lâché le système
vaut :
m = 100 g ; g = 10 SI ; a
= 30° ; k = 20 N/m.
A) d = 5 cm. Vrai.
m = 0,10 kg
; d = 2*0,10
*10 *0,5 / 20 =0,05 m = 5 ,0 cm .
B) d = 4 cm. Faux. C)
d = 3
cm. Faux ; D) d = 2 cm. Faux ; E) d = 1 cm. Faux.
F) Aucune proposition ne convient.
Faux.
Question 3.
Le graphe qui représente l'énergie cinétique du bloc en fonction
de la distance parcourue est :
A) Une droite. Faux.
Conservation de l'énergie
mécanique à une date t : 0 = ½mv2 +½kx2 -mg
x sin a.
½mv2 = -½kx2 +mg x sin a.
B) Une droite qui
passe par l'origine. Faux.
C) Un cercle. Faux.
D) Une parabole.Vrai.
E) Une sinusoïde. Faux.
F) Aucune proposition ne convient. Faux.
Question 4.
Quand le bloc a parcouru 2 cm sur la plan incliné, son énergie
cinétique vaut :
A) 7 mJ. Faux.
½mv2 = -½*20 *0,022 +0,10 * 10 *0,02
*0,5 =-0,004 +0,01 =0,066 J = 6 mJ.
B) 6 mJ. Vrai.
C) 5 mJ. Faux. D) 4 mJ. Faux. E) 3 mJ. Faux. F) Aucune proposition ne
convient.
Question 5.
Quand le bloc a
parcouru 2 cm sur la plan incliné, son énergie cinétique dans le
système international peut s'écrire :
A)
0,01 mg sin a-0,2k. Faux.
-½k 0,022 +mg 0,02 sin a = -2 10-4
k+0,02 mg sin a.
B) 0,05 mg sin a-0,2k. Faux.
C) 0,1 mg sin a-0,2k. Faux.
D) 0,1 mg sin a-0,2k.
Faux.
E) 0,1 mg sin a-0,1k. Faux.
F) Aucune
proposition ne convient. Vrai.
|
.
|
.
Plan incliné.
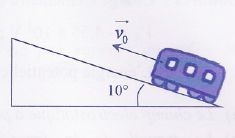
Le wagon de queue d'un train se détache alors qu'il aborde une côte à
la vitesse V0= 30 m/s. La masse du wagon et des voyageurs
est de 170 tonnes, la voie fait un angle de 10° avec 1'horizontale. Les
roues du wagon sont freinées par un frottement solide d'intensité
constante F = 221 kN. Une fois immobilisé, le wagon redescend.
g sin 10 ~1,7 m s-2 ; 172 =289 ; 4*17 = 68 ;
51/17 = 3 ; 221/170=1,3 ; 170/221 ~ 0,77.
Le frottement solide est présent lors de la montée et de la descente
avec la même intensité.
Données :
a) L'unité du Newton est kg.m-1.s-2. Faux.
Une force est une masse
fois une accélération : kg m s-2.
b) Le wagon va s'arrêter au bout d'environ 10 secondes. Vrai.
Sur un axe parallèle au plan et dirigé vers le haut :

c) Le travail du poids est moteur lors de la descente. Vrai.
d) Lors de la descente, la valeur de l'accélération du wagon est de 3
m.s-2. Faux.
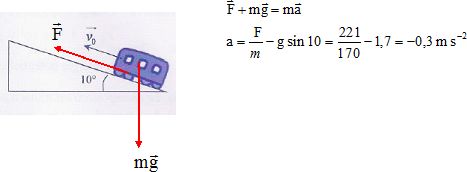
Sur un axe parallèle au plan et dirigé vers le
haut :
 |
|
Mouvement
sur
un plan incliné.
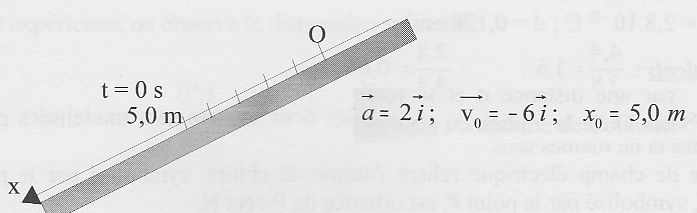
La bille ponctuelle M est lancée vers le haut.
A)
Le mouvement de
la bille est uniformément varié. Vrai.
B) La position de M est donnée par x(t) = -t2
+6t +5. Faux.
Suivant
l'axe proposé : a
= 2 m s-2 ; v = at + v0
= 2t -6 ; x = ½t2 + v0t + x0
= t2 -6 t + 5.
C) La bille passe en O aux dates t1 = 1,0 s et t2
= 5,0 s avec une vitesse de norme 4,0 m/s. Vrai.
t2 -6 t + 5 = 0 ; D = 36-20 = 16 ; t1
=(6-4) 2 = 1 ; t2 =(6+4)/2 = 5 s.
v = 2-6 = -4 m/s et v = 2*5-6 = 4 m/s.
D) Pour t < 3,0 s, la bille s'élève en ralentissant. Vrai.
Au point le
plus haut la
vitesse est nulle ; 0 = 2t-6 soit t = 3 s.
E) Pour t = 3 s, la bille est au sommet de sa trajectoire avec une
vitesse non nulle.
Faux.
La bille est au point le plus
haut avec
une vitesse nulle.
|
|