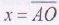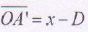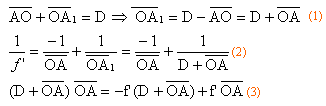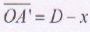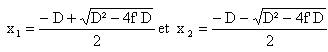.
|
Question 12.
En appliquant la formule de conjugaison de Descartes, on trouve une
équation du seconde degré entre x, D et f ' qui est :
A) x2 +Dx -f ' D = 0. Faux.
(2) réduction au même dénominateur ; les dénominateurs étant égaux, il y a
égalité entre les numérateurs.
D'où en effectuant : -D x +x2 = -f ' D +f ' x - f ' x ;
x² - Dx + f 'D=0.
B) x2 +Dx +f 'D =0. Faux.
C) x2 -Dx -f 'D =0. Faux.
D) -x2 +Dx +f 'D =0. Faux.
E) x2 -D2x = -f 'D . Faux.
F) Aucune proposition ne convient. Vrai.
Question
13.
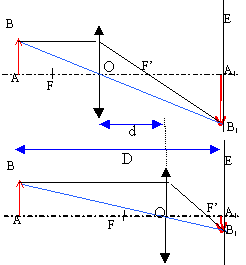
Les deux positions de la lentille permettant d'obtenir une image sur
l'écran sont notées x1 et x2. On pose d = x1-x2,
d est une distance.
A) Pour obtenir les deux positions précédentes, on doit vérifier la
relation : D2 + 4f 'D >0. Faux.
Résoudre l'équation du second degré : D= D²-4f 'D. Le discriminant est positif si
D >4f '.
B) Pour obtenir les deux positions précédentes, on
doit vérifier la relation : D2 - 4f 'D =0. Faux.
Dans ce cas, une seule
position est possible.
C) On peut écrire
que f ' = (D2-d2) / (4D). Vrai.
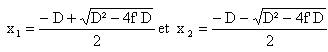
La différence x1-x2
est égale à d.
Elever au carré d'où : d²
= D²-4f'D soit (D²-d²) / (4D) = f '.
D) On peut écrire que f ' = (D2+d2)
/ (4D). Faux.
E) On peut écrire que f ' = -(d2-D2)
/ (4D). Vrai.
F) Aucune proposition ne convient. Faux.
|
|
Question 14.
Pour D = 2,0 m, on trouve d = 1,4 m.
A) La vergence de la
lentille est C = 8,0 dioptries. Faux.
f ' =(4-1,42)
/ 8 =0,25 m = 25 cm ; C = 1 / f ' = 1/0,25 = 4 dioptries.
B) La vergence de la
lentille est C = 10 dioptries. Faux.
C) f ' = 10 cm. Faux.
D) f ' = 12,5 cm. Faux.
E) f ' = 25 cm. Vrai.
F) Aucune proposition ne convient. Faux.
Question
15.
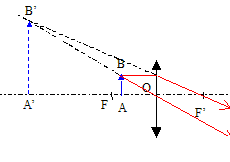
On place maintenant un objet réel à 10 cm de la lentille précédente.
A) L'image obtenue est virtuelle. Vrai.
L'objet est situé entre
le centre optique O et le foyer objet : la lentille fonctionne en
loupe.
B) L'image esr
réelle. Faux.
C) L'image obtenue est rejetée à l'infini. Faux.
D) L'image obtenue est droite. Vrai.
E) L'image obtenue est rétrécie. Faux.
F) Aucune proposition ne
convient.
|
|