|
|
|
|
Dans
cet exercice, seules les valeurs numériques des grandeurs sont
demandées.
Sur une large avenue, trois automobilistes, assimilées à des points
matériels, roulent côte à côte avec la même vitesse v0
= 12 m/s. A l'instant t=0, ils sont à la distance d = 300 m d'un feu de
croisement lorsque celui-ci passe instantanément au rouge.
- Le premier automobiliste, A1, commence à
ralentir immédiatement et s'arrête au feu à l'instant t1
où celui-ci repasse au vert.
- Le second, A2, ne commence à freiner qu'à 60 m
du feu et s'arrête à son niveau à l'instant t2.
- La durée du freinage du troisième, A3, est de
20 s. Il s'arrête au feu à l'instant t3.
On suppose que le mouvement de chaque automobiliste est uniformément
retardé pendant les phases de freinage.
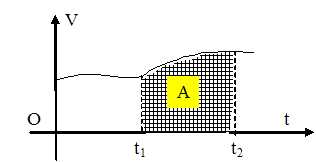
On admet que, sur un diagramme des vitesses ( schéma reprsentant la
vitesse v d'un mobile en fonction du temps ), la distance parcourue par
un mobile entre les instants t1 et t2
et égale à l'aire A sous la courbe V(t) entre ces deux instants.
Etude
du mouvement de A1.
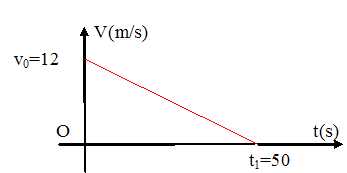
Donner
la valeur de t1 et
représenter son diagramme des vitesses.
Décélération a1 < 0 ; 0-v02
= 2a1d ; a1 = -v02
/(2d ) = -122 / 600 = -0,24 m s-2.
Vitesse : v1 = a1t + v0
= -0,24 t +12 ;
0 = -0,24 t1 +12 ; t1 =
12/0,24 = 50 s.
|
.
|
Etude
du mouvement de A2.
A quel
instant t'2 l'automobiliste commence t-il à
freiner ?
Il parcourt d-60 = 300 -60 = 240 m à la vitese v0
= 12 m/s.
t'2 = 240/12 = 20 s.
Quelle
est la durée du freinage Dt'2
?
Décélération a2
< 0 ; 0-v02 = 2*60a2
; a2 = -v02
/120 =-122 / 120 = -1,2 m s-2.
Vitesse : v2 = a2t + v0
= -1,2 t +12 ;
0 = -1,2 Dt'2
+12 ; Dt'2 = 12/1,2 = 10 s.
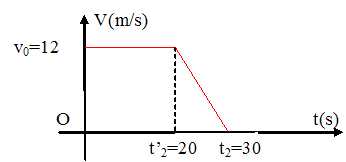
Représenter
son diagramme des vitesses.
|
|
Etude
du mouvement de A3.
A quelle
distance d3 l'automobiliste commence t-il à
freiner ?
d3 + 120 = 300 ; d2
= 180
m.
A quel
instant t'3 l'automobiliste commence t-il à
freiner ?
12 t'3 = 180 ; t'3 =180/12 = 15 s.
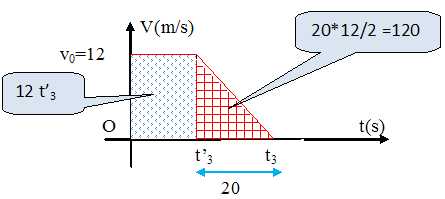
Calculet t3,
son instant d'arrêt et représenter son diagramme des vitesses.
t3 20+15 = 35 s.
|
|