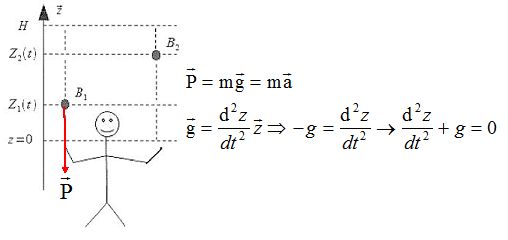Le jongleur : concours technicien supérieur 2012. Ministère du développement durable des transports et du logement. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .  Un jongleur jongle avec deux balles de même masse notée m. Il lance chaque balle verticalement. Lorsque la première balle atteint le sommet de sa trajectoire, il lance la seconde. Lorsque la seconde atteint le sommet de sa trajectoire, le jongleur lance à nouveau la première balle vers le haut ( en supposant qu'il a réussi à la rattraper entre temps  bien sûr). A chaque fois, on suppose que le jongleur lance les balles avec une même vitesse v0. On supposera les balles ponctuelles et on notera les deux points associés respectivement B1 pour la première balle et B2 pour la seconde. Dans tout l'exercice le référentiel est supposé galiléen et on appelle (oz] l'axe vertical orienté vers le haut et z le vecteur unitaire associé à cet axe. On ptrend z=0 pour l'altitude de la main du jongleur. Les balles partant vers le haut, leurs altitudes seront donc toujours positives. 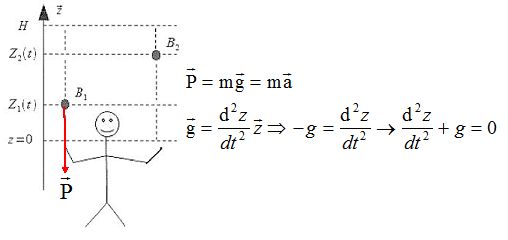Etude du premier lancer. On s'intéresse au lancer de la première balle B1. Faire l'inventaire de toutes les forces s'exerçant sur la balle une fois lâchée par le jongleur. Faire un schéma de la situation. On négligera le frottement de l'air. La balle est soumise à son poids et à la poussée d'Archimède due à l'air. Or la masse volumique de l'air est bien inférieure à la masse volumique de la balle : la poussée est donc négligeable devant le poids. Comment s'appelle un tel mouvement ? la balle n'étant soumise qu'à son poids, la chute est dite libre. Le mouvement est vertical uniformément accéléré. Etablir l'équation différentielle caractérisant le mouvement de la balle. Voir schéma ci-dessus. Déterminer l'expression de la vitesse v1(t) de la balle. La vitesse est une primitive de l'accélération : v1(t) = -gt + constante. La vitesse initiale est v0 : v1(t) = -gt + v0. En déduire l'expression de z1(t). La position est une primitive de la vitesse et la position initiale est l'origine de l'axe : la constante d'intégration est donc nulle. z1(t) = -½gt2 + v0t. Déterminer l'instant ts pour laquelle la balle atteint le sommet. Au sommet, la vitesse de la balle est nulle : 0 = -gts+v0 ; ts = v0/g. On appelle H la hauteur à laquelle le jongleur envoie la balle. Déterminer H. H = -½gts2 + v0 ts. H = -½g(v0/g)2 + v0 (v0/g) = ½v02 / g. Le jongleur veut envoyer la balle à un mètre de hauteur. Si on prend g = 10 m s-2, calculer v0 et ts. On donne racine carrée (5) ~2,2. v0 = (2gH)½ = (2*10*1)½ =(22*5)½ = 2 * 5½ ~2*2,2 = 4,4 m/s. ts = v0/g~4,4 /10 ~0,44 s.   . Etude du second lancer et du croisement. Le jongleur lance la seconde balle lorsque la première atteint le somme de sa trajectoire. Le mouvement de la seconde balle débute donc lorsque t = ts. Pourquoi l'équation différenteille de la seconde balle sera-t-elle la même que celle de la première ? La seconde balle, comme la première, n'est soumise qu'à son poids. Les deux balles sont lancées vers le haut avec la même vitesse v0. Les conditions initiales sont désormais les valeurs de la vitesse v2(t)  = v0 et de l'altitude z2(t) de la seconde balle pour t = ts, soit z2(t) = 0. En déduire l'expression de v2(t). v2(t) = -g(t-ts) + v0. v2(t) =-gt +gts +v0 = -gt +g ( v0/g) + v0 = -gt + 2v0 avec t supérieur ou égal à ts. Déterminer l'expression de z2(t). z2(t) = -½g(t-ts)2 + v0(t-ts). Calculer tc, instant pour lequel les balles se croisent, en fonction de ts. z2(tc)= z1(tc)  ; -½g(tc-ts)2 + v0(tc-ts)= -½gtc2 + v0tc. ½gtc2- ½g(tc-ts)2 + v0(tc-ts)- v0tc=0. ½g [tc2-(tc-ts)2 ]- v0 ts=0 ; ½g(tc-(tc-ts) ) (tc+(tc-ts))- v0 ts=0. ½g ts (2tc-ts)- v0 ts=0 ; ½g (2tc-ts)- v0=0 ; 2tc-ts = 2v0/g ; tc = v0/g + ½ts = ts + ½ts =  1,5 ts ~ 1,5 *0,44 ~ 0,66 s. Calculer Hc, hauteur à laquelle les balles se croisent en fonction de H. Il sera intéressant pour cela de déterminer z1(1,5 ts). z2(tc)= z1(tc) =Hc ; Hc = -½g(1,5 ts)2 + v0(1,5ts) = 2,25 (-½g) ts2 +1,5 v0 ts ; or ts = v0/g, d'où : Hc =2,25 (-½g) (v0/g)2 +1,5 v0 (v0/g) = -1,125 v02/g +1,5 v02/g = 0,375 v02/g ; or H =  ½v02 / g d'où :  Hc =0,375 *2H = 0,75 H= 0,75 m. Jonglage réel. En réalité, les balles ne sont pas ponctuelles et il faut prendre en compte les frottements de l'air. Sans aucun calcul et uniquement qualitativement, que peut-on dire des hauteurs réelles H et Hc par rapport aux valeurs calculées ? L'énergie mécanique de chaque balle diminue du travail des frottements : initialement cette énergie est sous forme cinétique ½mv02 ; au point le plus haut, elle se trouve sous forme potentielle de pesanteur mgH. Sans frottement : ½mv02 = mgH ; avec frottement : ½mv02  mgH' - ½mv02= travail négatif des frottements. mgH'-mgH < 0 ; H' < H. De même H'c < Hc. De même que peut-on dire des instants ts et tc par rapport aux valeurs calculées ? Sans frottement : v1(t) = -gt + v0 ; avec frottement l'accélération, notée "a" est inférieure à g, en conséquence , au point le plus haut : t's = v0/ a, supérieur à ts. Il en sera de même pour t'c : t'c >tc. Quel peut être l'intérêt pour le jongleur de lancer les balles d'une main à l'autre ? Cela permet de lancer la seconde balle au bon moment, dès que la première atteint le point le plus haut. .

menu