|
|
|
|
Un
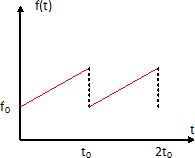
émetteur embarqué dans l'avion délivre un signal sinusoïdal s(t) modulé
en fréquence. Ce signal se propage verticalement à la célérité c = 3,00
108 m/s. Il ne sera pas tenu compte du déphasage dû à la
réflexion ni également de l'effet Doppler. Une antenne fixée sur
l'avion permet à l'altimètre de mesurer son altitude z à partir du
temps mis par l'onde radioélectrique pour effectuer un aller-retour
entre le sol et l'avion.
Le signal s(t) est de la forme s(t) = A cos q(t) tel que la fréquence instantanée f(t) = 1/(2p) dq/dt varie au cours du temps avec la période t0. Plus précisément f(t) varie en dent de scie : c'est à dire que pour 0<= t < t0 la fréquence vérifie l'équation f(t) = f0 + t df/t0.
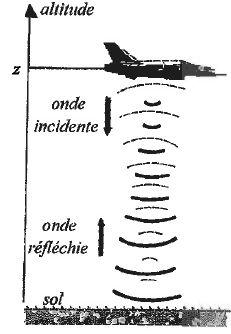
Représenter le graphe des variations de la fréquence f(t) sur quelques périodes.
Par la suite on prendra f0 = 104 MHz, df = 100 MHz et t0 = 10 ms.
Sachant que s0 = A, déterminer l'expression de s(t) en fonction de w0 = 2pf0, w1 = df / (2f0t0), A et t.
On admet que l'on a toujours df << f0 et t < t0.
dq/dt = 2 p (f0 + t df/t0). Intégrer entre 0 et t :
q(t) = 2 p f0 t + p df / t0 t2 +B avec B une constante.
q(t) =w0t +2pw1f0 t2 +B.
s(0) = A = cos B ; B = cos-1(A).
s(t) = cos ( w0t +2pw1f0 t2 +cos-1(A)).
Le signal réfléchi par le sol puis capté par l'antenne de l'altimètre peut se mettre sous la forme r(t) = a s(t-t) où le paramètre t est positif et homogène à un temps.
Après avoir la signification physique dea paramètres a et t, déterminer l'expression de t en fonction de l'altitude z de l'avion et de la célérité c de l'onde radio. A.N : z = 3000 m.
a : amplitude de l'onde réfléchie ; t : durée de l'aller-retour entre l'avion et le sol.
t = 2z / c =6000 / 3 108 = 2,0 10-5 s = 50 µs.
|
Traitement du signal.
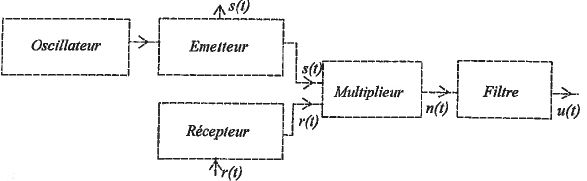
Montrer
que le signal de sortie du multiplieur n(t) peut s'écrire comme la
somme de deux sinusoïdes dont l'une possède une fréquence instantanée f1 fixe et l'autre une fréquence instantanée qui varie avec t. Exprimer ces fréquences en fonction de t, t, df, t0 et f0.
n(t) = k s(t) r(t) avec k une constante.
n(t) = k a s(t)s(t-t) = kaA cos q(t) A cos q(t-t) = ½kaA( cos (q(t)-q(t-t)) + cos(q(t)+q(t-t)).
q(t) =w0t +2pw1f0 t2 +B ; q(t-t) =w0(t-t) +2pw1f0 (t-t)2 +B.
q(t)-q(t-t) =w0t +2pw1f0 t(t-2t) = w0t -2pw1f0 t2-4pw1f0 t t.
Par suite 2pf1 = 4pw1f0 t ; f1 = 2w1f0 t = df / t0 t = 108 / 0,01 t = 1010 t.
q(t)+q(t-t) =w0t +2pw1f0 t(t-2t) =w0(2t-t) + 2pw1f0(t2+(t-t)2)= -w0t +2pw1f0t2+2w0 t +4pw1f0t2- 4pw1f0 t t =-w0t +2pw1f0t2+(2w0+4pw1f0t - 4pw1f0 t) t.
La fréquence variable vaut : w0/ p +2w1f0t - 2w1f0 t = 2f0 +df / t0 t -df / t0 t =2,08 108 +1010 (t -t).
|
On a presque toujours t <= 100 µs.
Quel
type de filtre doit-on utiliser et comment le qualibrer pour obtenir un
signal de sortie u(t) qui détermine facilement l'altitude de l'avion ?
f1 est inférieure à 106 Hz ( 1 MHz ) ; f1 = 2 1010 z / c = 2 1010 z / ( 3 108) ~ 67 z.
Il faut éliminer le signal de fréquence variable qui est l'ordre de 300 MHz.
Il faut utiliser un filtre qui supprime les fréquences supérieures à
quelques MHz, c'est à dire un filtre passe bas du premier ou du second
ordre dont la
fréquence de coupure est voisine de 5 106 Hz :
- dans le cas d'un ou deux dipoles RC : 1/ (2pRC) ~5 106 soit RC ~3 10-8 s.
- dans le cas d'un dipole RLC avec tension de sortie mesurée aux bornes du condensateur : f0 = 1/(2p (LC)½) = 5 106 soit LC ~10-15.
Parmi les filtres suivants, quel est celui qui vous paraît le plus adapté à l'application d'altimétrie étudiée précédemment ?
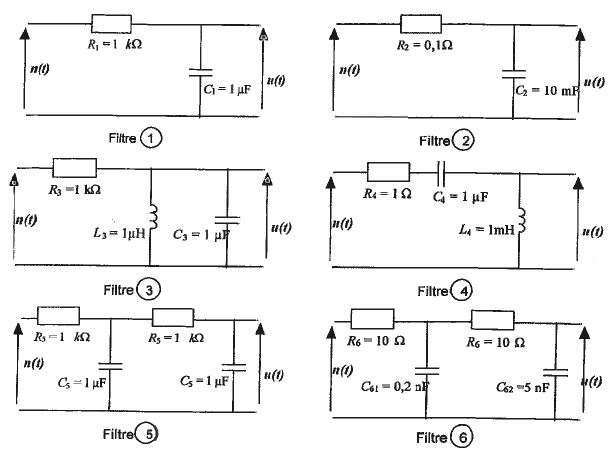
Le filtre 6 paraît le plus approprié.
|
Altimètre barométrique.
L'atmosphère terrestre est assimilée à un gaz parfait, de masse molaire
M = 29 g/mol, placé dans le champ de pesanteur uniforme, de valeur g =
10 m s-2. L'air est en équilibre stratifié, c'est à dire que
la pression P, la température T et la masse volumique µ sont fonction
de l'altitude z. Au sol P0 = 1,0 bar, T0 = 273 K.
Le référentiel lié à la terre est supposé galiléen, l'axe Oz est vertical ascendant, l'origine est prise au niveau du sol.
Montrer que l'équilibre mécanique implique : dP = -µgdz.
On
considère une particule de fluide au repos dans le champ de pesanteur
uniforme, de forme cubique dont les arètes ont pour longueur dx, dy, dz.
Volume de la particule dv = dxdydz ; la masse volumique du fluide étant notée µ, la masse de cette particule est : dm = µdxdydz.
La particule est au repos sous l'action de deux forces opposées, son
poids P = dm g et les forces pressantes de la part du fluide entourant
la particule.
Sur les faces latérales du cube, les forces pressantes sont opposées.
Sur les faces inférieure et supérieure, aux cotes z et z + dz, de surface dxdy, les forces pressantes sont : df1 = P(z) dxdy, verticale, orientée vers le haut et df2 = P(z+dz) dxdy, verticale, orientée vers le bas.
Par suite : -µgdxdydz +P(z) dxdy - P(z+dz) dxdy =0.
-µgdz + P(z)- P(z+dz) =0 ; P(z+dz) - P(z) = dP = -µgdz.
L'état stationnaire thermodynamique résulte d'une évolution régie par l'équation P µ-7/5 = P0 µ0-7/5= Cste.
Montrer qu'un altimètre barométrique est étalonné suivant la loi P(z) = P0(1-az)ß. Donner les valeurs numériques de a et ß.
µ = (P/Cste)5/7 ; dP = -(P/Cste)5/7 g dz ; dP / P5/7 = -Cste-5/7 gdz.
Intégrer : 3,5 P2/7= -Cste-5/7 g z + B avec constante. B = 3,5 P02/7.
3,5 (P2/7-P02/7) = -Cste-5/7 g z = -P0-5/7µ0 g z.
P2/7= P02/7-P0-5/7µ0/ 3,5 g z =P02/7(1-P0-1µ0/ 3,5 g z).
P = P0(1-P0-1µ0/ 3,5 g z)3,5.
a = P0-1µ0/ 3,5 g ; P0 V0 = m/M RT0 ; µ0 =m/V0 = P0 M / (RT0) =105*0,029/(8,31*273) =1,28 kg m-3.
a =1,0 10-5 *9,8*1,28 / 3,5 = 3,4 10-5 m-1.
|
|



