|
|
|
|
En
1641, un an avant sa mort, Galilée tente d'apliquer ls oscillations des
pendules au mécanisme de l'horloge.Les premières horloges électriques
apparaissent au milieu du XIX éme siècle. Aujourd'hui le quartz et
l'atome remplacent le mécanisme de l'horloge. L'horloge à quartz
utilise un oscillateur à quartz pour définir le temps.
Etude
d'un oscillateur électrique en régime libre.
Un dipole AB est constitué d'un
conducteur ohmique de résistance R, d'une bobine d'induction L, de
résistance négligeable et d'un condensateur de capacité C branchés en
série. Ce dipole est relié à un commutateur à deux voies K. En position
1, lecondensateur se charge sous la tension E délivrée par le
générateur de tension constante. Le condensateur une fois chargé, on
bascule à l'instant t=0 le commutateur K en position 2.
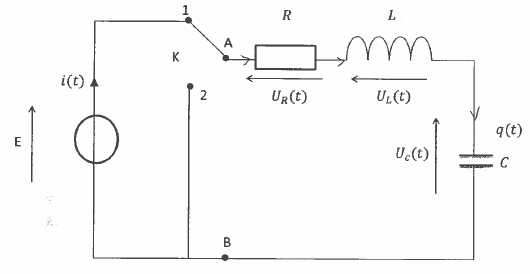
Ecrire les
relations entre Uc(t) et q(t), puis entre i(t)
et q(t).
Uc(t) =
q(t) / C ; i(t) = dq(t) / dt.
Exprimer
la tension aux bornes de la bobine.
UL(t) = Ldi(t)/dt = Ld2q(t)/dt2
= LC d2Uc(t)/dt2.
Exprimer
la tension aux bornes de la résistance.
UR(t) = R i(t) = Rdq(t) / dt = RC dUc(t)/dt.
Montrer
que l'équation différentielle vérifiée par Uc(t) en
fonction du temps s'écrit :
U"c(t) + w0
/ Q U'c(t) +w02
Uc(t) =0.
Q : facteur de qualité du circuit ; w0
: pulsation propre du circuit.
Additivité des tensions : Uc(t)
+UL(t)+UR(t)
=0.
Uc(t)
+ LC d2Uc(t)/dt2
+RC dUc(t)/dt
=0.
1/(LC) Uc(t)
+ d2Uc(t)/dt2
+R/ L dUc(t)/dt
=0.
d2Uc(t)/dt2
+ R/ L dUc(t)/dt
+ 1/(LC) Uc(t)
=0.
On pose w02
= 1/(LC) ; R / L = w0
/ Q soit Q = w0
L / R.
En déduire
l'expresion de la période propre T0.
T0 = 2p/w0
= 2p(LC)½.
L'oscillateur RLC se comporte comme un oscillateur amorti. On cherche
des solutions de l'équation différentielle du type : r2
+2lr +w02=0
avec l = w0
/(2Q).
Suivant le signe du discriminant, il existe 3 régimes différents.
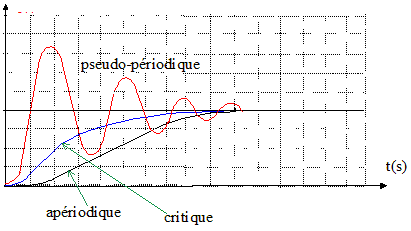
Nommer
chacun de ces 3 régimes et donner l'allure des variations de Uc(t)
dans le cas d'un discriminant négatif. D =4l2
-4w02.
D
> 0 : régime apériodique ; D
= 0 : régime critique ; D
< 0 : régime pseudopériodique.
|
.
|
Etude d'un oscillateur électrique en régime forcé.
Le
dipole AB est maintenant alimenté par un générateur basse fréquence,
supposé idéal, qui délivre une tension alternative sinusoïdal u(t) de
valeur efficace U0 :
u(t) = 2½U0 cos ( (wt).
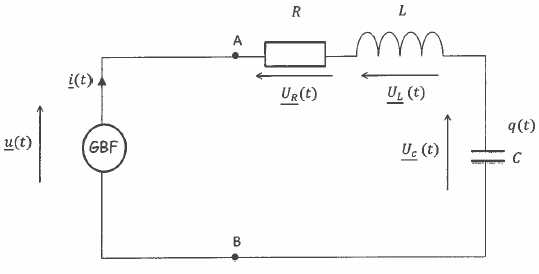
Etude de la fonction de transfert d'un circuit RLC série.
Donner l'expression de l'impédane complexe Zc du condensateur.
Zc =1 / (jCw).
Donner l'expression de l'impédane complexe ZL de la bobine.
ZL = j Lw.
En déduire l'expression de la fonction de transfert H(w) = Uc(t) / u(t) en fonction de R, L, C et w.
u(t) =(R + j Lw +1 / (jCw) ) i(t) ; Uc(t) = 1 / (jCw) i(t) ; H(w) = 1 / [(R + j Lw + 1/ (jCw) )(jCw)].
H(jw) =1/ ( jRCw -LCw2+1 ) = 1 / ( jRCw +1 - LCw2).
On pose w0 = 1/(LC)½, x = w / w0, Q = Lw0/R.
Montrer que H(jw) =1/(1+j x/Q +(jx)2).
- LCw2 = j2(w / w0)2 =(jx)2 ; C = 1 / (Lw02) ; jRCw = jRw / (Lw02) =j x/Q.
Par suite : H(jw) =1/(1+j x/Q +(jx)2).
|
En déduire l'expression du déphasage f en fonction de x et Q.
f = argument de la fonction de transfert : tan f = -x/Q / (1-x2) = -x/((1-x2)Q).
Exprimer
le gain G=||H|| = |H(jw)| en fonction de x et Q.
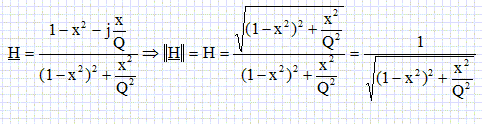
Il
peut exister une résonance en tension aux bornes du condensateur où le
gain passe par un maximum pour une certaine valeur de xr =w0/wr.
Déterminer l'expression de xr en fonction de Q.
dG/dx = -½(-4x(1-x2) +2x/Q2) / ((1-x2)2 +x2/Q2)3/2 ; cette dérivée s'annule pour : -4x(1-x2) +2x/Q2=0 ; 2(1-x2) =1/Q2
1-x2 =1/(2Q2 ) ; x2 = 1-1/(2Q2 ) ; xr =[ 1-1/(2Q2 )]½.
x étant positif, on ne retient pas la valeur négative.
En déduire l'expression de wr en fonction de w0 et de Q.
wr =w0 /xr =w0 [ 1-1/(2Q2 )]-½.
|
|