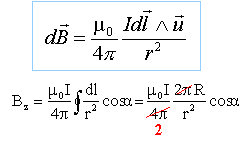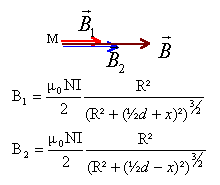|
|
|
|
Champ magnétique créé par une bobine plate.
On
considère une spire circulaire de centre O, de rayon R, parcourue par
un courant I. On cherche à calculer le champ magnétique b créée en un
point M quelconque de son axe.
Par conditions de symétrie, donner la direction de ce champ en M.
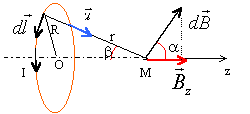
Tout plan passant par Oz est un plan
d'antisymétrie du système. En
conséquence le champ magnétique est
porté par l'axe Oz.
Exprimer le champ magnétique Bx créé en M en fonction de µ0, I, R, OM=x et dl.
On applique la relation de Biot et Savart :
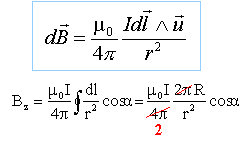
avec cos a = sin b,
angles complémentaires.
r = R / sin b ; cos a =R / r = R /(R2+z2)½.
On pose B0 =µ0I / (2R) ; Bz = B0[ R2/(R2+z2)]3/2.
Ce résultat pourra être admis pour les questions ultérieures.
Que représente B0 ?
B0 représente le champ magnétique créé au centre O de la spire.
On remplace maintenant la spire par une bobine plate de même rayon R, constituée de N spires.
Qu'appelle-t-on bobine plate ?
Le rayon de la bobine est très supérieure à la longueur ( épaisseur ) de la bobine.
Quelle est, dans ce cas, l'expression de B0 ?
B0 =Nµ0I / (2R)
|
.
|
Champ magnétique créé par deux bobines.
Soient deux bobines plates identiques, de rayon R, constituées de N spires et séparées d'une distance d =O1O2 = R. Elles sont toutes deux parcourues par un même courant I. On note B1(M) et B2(M)
les champs magnétiques crés respectivement par les bobines 1 et 2 et
B(M) le champ magnétique total en un point M. On nomme O le milieu du
segment O1O2.
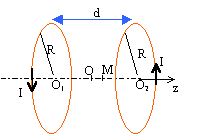
Exprimer les champs magnétiques B1(O), B2(O), B1(O2), B2(O2) en fonction de B0.
En O, z = ½R : B1(O) =B2(O)= NB0[ R2/(R2+0,25R2)]3/2=NB0(1/1,25)3/2=NB0(0,8)3/2=0,716NB0.
En O2, z = R : B1(O2) =NB0[ R2/(R2+R2)]3/2=NB0(1/2)3/2=0,354N B0.
B2(O2) =NB0.
Montrer que B(O) et B(O2) peuvent s'écrire sous la forme : B(O) = a B0 et B(O2) = ß B0. Donner les valeurs de a et ß.
En prenant O pour origine de l'axe horizontal et un point M, d'abscisse x, situé entre O et O2.
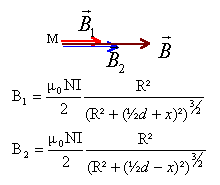
Les champs crées par chaque bobine ont la
même direction et le même sens; le champ
résultant est la somme vectorielle des champs
crées par chaque bobine.
En O : B(O) = B1(O) +B2(O) = 2*0,716 NB0 =1,43 NB0.
En O2 : B(O2) = B1(O2) +B2(O2) = (0,354 +1) NB0 =1,35 NB0.
|
Déterminer la valeur du taux de variation du champ DB / B lorsque l'on passe du point O au point O2.
DB/B =(1,43-1,35) / 1,4 ~0,057 ( 5,7 % ).
Conclure quand à la nature du champ entre les bobines.
Le
champ garde toujours la même direction et le même sens ; de plus sa
valeur est pratiquement constante ( à 6 % près ). Ce champ magnétique
est donc uniforme sur l'axe, entre les bobines distantes de d=R.
|
|