|
|
|
|
L'aventurier
autrichien Felix Baumgartner est devenu dimanche 14 octobre 2012 le
premier homme à franchir le mur du son en chute libre après s'être
lancé d'une capsule accrochée à un ballon d'hélium d'une altitude
reccord d'un peu plus de 39,0 km dans le ciel du Nouveau-Mexique.
On peut décomposer ce saut en trois phases :
1ère phase
: elle commence lorsque le parachutiste se laisse tomber sans vitesse
initiale de sa capsule et se termine lorsqu'il atteint la vitesse
maximale vmax = 1,34 103 km/h. Les frottements et la poussée d'Archimède sont négligés durant cette phase.
2ème phase
: elle débute lorsque la vitesse maximale est atteinte. Il existe alors
une force de frottement de type f = kv due à l'air. On négligera la
poussée de l'air sur le parachutiste.
3ème phase : elle débute lorsque le parachutiste ouvre son parachute. Elle ne sera pas étudiée ici.
Etude de la variation de la constante de pesanteur.
le parachutiste M tombe d'une hauteur h par rapport à la terre. On peut assimiler la terre comme un objet ponctuel de masse MT, sa surface se trouvant à une distance RT
du centre O. On se propose d'étudier les variations de la constante de
pesanteur g lors de la chute du parachutiste M entre sa hauteur de
départ et le sol.
Rappeler
l'expression vectorielle de la force gravitationnelle exercée par la
terre sur un corps de masse m séparés d'une distance D.
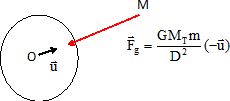
Rappeler l'expression vectorielle du poids dans ces conditions.
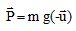
En déduire l'expression de la constante de pesanteur g en fonction de MT, G et D.
g = GMT /D2.
On donne RT =6,38 103 km , h = 39,0 km, G =6,67 10-11 SI, MT = 5,98 1024 kg.
Exprimer puis calculer g dans le cas où :
- Le parachutiste est à la surface de la terre.
g1 = GMT /RT2 = 6,67 10-11 *5,98 1024 / (6,38 106)2 =9,80 m s-2.
- Le parachutiste est à la hauteur h de la terre.
g2 = GMT /(RT+h)2 = 6,67 10-11 *5,98 1024 / (6,38 106+ 39,0 103)2 =9,68 m s-2.
Exprimer la varaition relative (g1-g2) / g1 en fonction de RT et h. La calculer et conclure.
(g1-g2) / g1 =1-(RT / (RT+h))2 =1-1/(1+h/RT)2 = 1-1/(1+39/6380)2=0,0121 ( 1,21 %).
Cette variation relative étant très faible, g peut être considéré comme constant sur cette distance.
|
.
|
Etude de la phase 1.
On cherche à déterminer la distance pour laquelleBaumgartner atteint sa
vitesse maximum. Le parachutiste M se laisse tomber sans vitesse
initiale d'une hauteur h, prise comme origine. Le référentiel est celui
de la terre considéré comme galiléen. On prendra g = 9,80 m s-2. L'axe vertical est orienté vers le bas.
Qu'est-ce que le mur du son ? Pourquoi peut-on dire que Felix Baumgartner l'a franchi avec ce saut ?
Lorsqu’un
avion vole en vitesse subsonique (vitesse inférieure à la célérité du
son dans l’air), il crée des ondes dites de pression qui se propagent à
la célérité du son (figure 1). Lorsqu’il accroît sa vitesse et qu’il
atteint la célérité du son, les ondes de pression s’accumulent devant
le nez de l’avion (figure 2). Lorsqu’il dépasse la célérité du son (on
dit qu’il passe le mur du son), il se produit alors des ondes de
compression et de dilatation qui provoquent ce fameux « bang »
perceptible à plusieurs dizaines de kilomètres à la ronde. Pour une
vitesse supérieure à la célérité du son, les ondes se propagent
derrière l’avion dans un cône appelé cône de Mach.
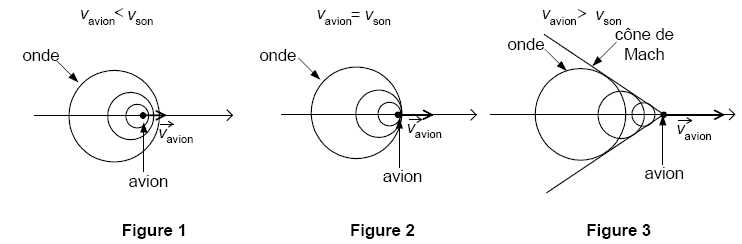
Felix Baumgartner a franchi le mur du son car vmax est supérieure à la vitesse du son.
En appliquant le principe fondamental de la dynamique, exprimer en fonction de g et t :
- L'accélération : lors d'une chute libre az(t) = g.
- La vitesse vz(t) : la vitesse est une primitive de l'accélération et la vitesse initiale est nulle, vz(t) = gt.
- La position z(t) du parachutiste : la position est une primitive de
la vitesse et la position initiale est l'origine de l'axe, z(t) = ½gt2.
Exprimer puis calculer la durée t1 pour laquelle vmax est atteinte en fonction de vmax et g.
t1 = vmax / g ; vmax =1,34 103 / 3,6 =372,2 m /s ; t1 =372,2 / 9,80 = 37,98 ~38,0 s.
Exprimer puis calculer la distance d pour laquelle vmax est atteinte en fonction de vmax et g.
d = ½g(vmax / g)2 =vmax2 / (2g) =372,22 / (2*9,80) =7,07 103 m = 7,07 km.
|
Etude de la phase 2.
On considère qu'à t=0 le parachutiste a une vitesse initiale v0 = vmax. On donne k = 16,9 kg s-1; masse du système m = 120 kg.
Montrer que la vitesse suit une équation différentielle du type dv/dt + v/t =g. Exprimer t en fonction de k et m.

Résoudre cette équation différentielle et montrer que la solution s'écrit sous la forme v(t) = A exp(-t / t) +B. Donner l'expression des constantes A et B.
Solution générale de dv/dt + v/t =0 : v =A exp(-t / t).
Solution particulière de dv/dt + v/t =g : vlim = t g.
Solution générale de dv/dt + v/t =g : v(t) =A exp(-t / t) + t g.
Condition initiale : v(0) = vmax = A + t g. par suite A = vmax -t g.
v(t) = (vmax -t g) exp(-t / t) + t g.
Donner l'expression de z(t).
z(t) est une primitive de la vitesse et la position initiale est à z(t1) =d.
z(t) = -t (vmax -t g) exp(-t / t) + t g t + cste.
z(0) = d = -t (vmax -t g) +cste ; cste = t (vmax -t g) +d.
z(t) = t (vmax -t g)(1- exp(-t / t)) + t g t +d.
On peut considérer que la vitesse limite est atteinte lorsque v(t) =1,01 vlim.
Exprimer et calculer le temps t2 pour lequel la vitesse limite est atteinte.
1,01 t g = (vmax -t g)exp(-t2 / t) + t g ; (vmax -t g)exp(-t2 / t) = 0,01t g.
0,01t g / (vmax -t g) = exp(-t2 / t) ; ln ( (vmax -t g) / (0,01t g)) = t2 / t.
t2 = t ln ( (vmax -t g) / (0,01t g)) avec t = 120 / 16,9 =7,10 s.
t2 =7,10 ln((372,2 -7,10*9,80) / (0,0710*9,80)) = 43,1 s.
En déduire la distance parcourue par le parachutiste.
z(t2) = t (vmax -t g)(1- exp(-t2 / t)) + t g t2 +d.
z(t2) =7,10(372,2 -7,10*9,80) (1-exp(-43,1 / 7,10)) +7,10*9,80*43,1 +7,07 103 =1,22 104 m = 12,2 km.
|
|