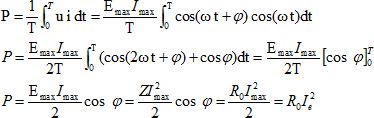|
|
|
|
Une bobine d'inductance L et de résistance r est alimentée par une source de courant continu sous une tension U1 = 6 V. Elle est traversée par un courant d'intensité I1
= 2 A. Lorsqu'on alimente cette même bobine par une source de courant
sinusoïdal de fréquence f = 50 Hz sous une tension efficace Ueff = 110 V, l'intensité efficace du courant vaut Ieff = 1 A.
Déterminer L et r.
En courant continu, la tension aux bornes de la bobine vaut U1 = r I1 ; r = U1 / I1 = 6 / 2 = 3 ohms.
En courant alternatif, la tension aux bornes de la bobine vaut Ueff = Z Ieff ; Z = Ueff / Ieff = 110 / 1 = 110 ohms.
Z2 =r2 + (Lw)2 avec w = 2 p f = 2*3,14 *50 = 314 rad/s.
(Lw)2 = Z2 - r2 =1102-9 =12091 ; Lw =109,96 ohms ; L = 109,96 / 314 = 0,35 H.
Cette
bobine est placée en série avec une résistance R = 50 ohms et un
condensateur de capacité C = 0,1 µF. On alimente l'ensemble par un
générateur basse fréquence de résistance interne RG = 50 ohms délivrant un signal sinusoïdal de pulsation w et de tension efficace constante Ee telle que e(t) = 2½Ee cos ( wt+f).
On souhaite étudiée la résonance en intensité du circuit.
Représenter le schéma du montage expérimental ainsi que les points de mesures.
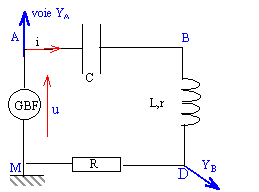
Exprimer l'impédance Z du circuit sous la forme Z = R0(1+jQ(x-1/x) avec x = w/w0.
Z = (R + RG + r) + j(Lw -1/(Cw)).
On pose w20 = 1/(LC) : Lw -1/(Cw) = L ( w-w20/w) = Lw0( w/ w0-w0/w) = Lw0(x-1/x).
On pose R0 =R + RG + r ; Z = R0 ( 1 + jLw0/ R0(x-1/x).
On pose Q =Lw0/ R0. par suite : Z = R0(1+jQ(x-1/x).
|
.
|
En déduire l'expression de l'intensité efficace sous la forme Ie(w) = a / (1+ß2(x-1/x)2)½.
Z = R0(1+Q2(x-1/x)2)½ ; Ie(w) = Ee / Z = Ee /R0 (1+Q2(x-1/x)2)-½.
On pose a = Ee /R0 ; ß = Q.
Montrer que Ie(w) présente un maximum pour w = wr. Préciser wr.
Dériver Ie(w) par rapport à w et chercher la valeur de la pulsation qui annule cette dérivée.
dIe(w) / dw = w0 dIe(w) / dx ; on pose v = x-1/x ; v' = 1+1/x2.
On pose u = 1+ß2v2 ; u' = 2ß2v v' =2ß2(x-1/x)(1+1/x2).
Ie(w) =a(u)-½ ; w0 dIe(w) / dx = -½w0 a u' u-3/2 = -w0 aß2(x-1/x)(1+1/x2)(1+ß2(x-1/x)2)-3/2.
La dérivée s'annule pour x= 1 soit wr = w0.
Pour w = 0 , Ie(0) = 0 ; pour w très grand : Ie(infini) = 0 ; il s'agit bien d'un maximum.
On appelle bande passante l'intervalle de pulsation Dw = w1 - w2 pour laquelle Ie(w) > Imax / 2½.
Montrer que Dw = w0 / Q.
Expression des pulsations de coupures, notées
w1 et
w2
:
Si I= I0 2-½ alors Z =
U0/I = 2½ U0/ I0
=2½ R
Or Z = R0 [1
+Q2(x-1/x)2
]½.
d'où 2 = 1
+Q2(x-1/x)2
1/ Q2 =
(x-1/x)2 ; x-1/x =+1/ Q et x-1/x
=-1/ Q
x2 -x/Q
-1 =0 ; solution positive x2 = 0,5( 1/
Q + [1/
Q2+4]½) ;
w2=
0,5w0
( 1/ Q0 + [1/
Q02+4]½)
x2 +x/Q
-1 =0 ; solution positive x1 = 0,5( -1/
Q + [1/
Q2+4]½) ;
w1=
0,5w0
( 1/ Q0 + [1/
Q02+4]½)
w2-
w1
= w0
/
Q.
|
On donne Ie en fonction de la fréquence f.
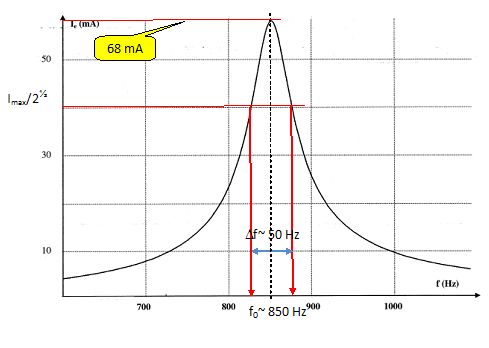
Déterminer L et r.
Imax ~0,068 A = Ee / R0. r = Ee /Imax -R-RG.
Q = f0 / Df0 = 850 / 50 = 17.
Q =Lw0/ R0. R0 ~ 103 ohms ; w0 = 2 p f0 = 6,28 *850 = 5340 rad/s ; L = 17*103 / 5340 = 0,33 H.
Etablir l'expression de la puissance moyenne dissipée dans le circuit.
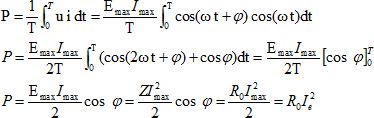
Exprimer la bande passante à partir de la puissance moyenne.
A la résonance :
Pmax =R0
I²e max.
Aux fréquences de coupures : Ie= Ie max 2-½ alors :
P = ½R0
I²e max = ½Pmax.
½R0
I²e max = R0
I²e = E02/ (R0 (1+Q2(x-1/x)2)).
Par suite : 2 = 1
+Q2(x-1/x)2
1/ Q2 =
(x-1/x)2 ; x-1/x =+1/ Q et x-1/x
=-1/ Q
x2 -x/Q
-1 =0 ; solution positive x2 = 0,5( 1/
Q + [1/
Q2+4]½) ;
w2=
0,5w0
( 1/ Q0 + [1/
Q02+4]½)
x2 +x/Q
-1 =0 ; solution positive x1 = 0,5( -1/
Q + [1/
Q2+4]½) ;
w1=
0,5w0
( 1/ Q0 + [1/
Q02+4]½)
w2-
w1
= w0
/
Q.
|
|