|
|
|
|
Principe d'un oscillateur optique : le laser.
La
cavité laser est constituée par un milieu amplificateur A contenu entre
deux miroirs plans parallèles M et M', distants de L. Des décharges
électriques, provoquées par une alimentation extérieure, donnent
naissances à des odes lumineuses de très faible amplitude.
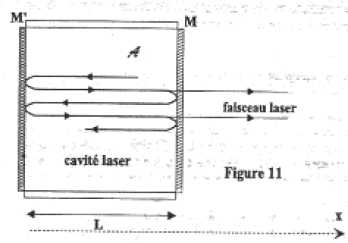
Le
miroir M réfléchit vers la cavité une partie de la lumière produite
dans le milieu, l'autre partie, constituant le faisceau laser, est
transmise vers l'extérieur. Au niveau de M, l'amplitude Ar de l'onde réfléchie est liée à l'amplitude Ai de l'onde incidente par la relation Ar = rAi avec 0 < r <1. Le miroir M' est, quant à lui, parfaitement réfléchissant. L = 0,200 m ; r = 0,998.
Après chaque aller-retour complet de l'onde, son amplitude est multipliée par un facteur g0>1.
Les molécules de A, grâce aux transitions entre les niveaux d'énergie,
amplifient l'énergie transportée par l'onde : A joue le rôle
d'amplificateur.
Condition d'accord de phase.
Les
ondes de fréquence f, de célérité c, effectuent entre M et M' un très
grand nombre d'aller-retour. Un laser ne peut émettre un faisceau que
si les ondes lumineuses sont en phase dans la cavité après un
aller-retour. On admet que cela se produit si la distance parcourue
lors d'un aller-retour est un multiple entier de la longueur
d'onde ; ceci constitue la condition d'accord de phase.
En déduire que seules certaines fréquences fp à préciser ( modes propres ), caractérisées par un nombre entier p non nul, sont émises avec un signal d'amplitude maximale.
2 L = p l ; f = c / l ; fp = p c / (2L).
Propriétés du laser.
Cohérence temporelle du laser.
Si
le laser fonctionne sur un de ses modes propres, il est susceptible
d'émettre une lumière monochromatique, c'est à dire de fréquence
parfaitement définie. Cette propriété est caractéristique de
l'excellence cohérence temporelle du laser. En réalité, la lumière
laser possède un petit étalement en fréquences df autour de la valeur calculée pour un mode propre. Cet étalement spectral provient des imperfections de la cavité elle-même.
En notant t le temps mis par la lumière pour faire un aller-retour dans la cavité, on peut montrer que : df = |lnr2| / t.
Calculer df.
t = 2 L/c = 0,400 / (3,00 108) =1,33 10-9 s ; df = |ln0,9982| / (1,33 10-9) =3,00 106 Hz.
Un
oscillateur excité sur l'une de ses fréquences propres présente une
réponse résonnante caractériséepar un nombre sans dimension appelé
facteur de qualité Q. Ce nombre qui vaut Q = fp/df caractérise l'acuité de la résonance.
Calculer Q si fp =4,74 1014 Hz.
Q = 4,74 1014 /(3,00 106) = 1,58 108.
A
titre de comparaison, on donne les ordre de grandeur de quelques
facteurs de qualité dans divers domaines de la physique. Q( circuit
électrique) ~ 10 ; Q ( sismographe ) ~ 1000 ; Q ( oscillateur quartz) ~
105.
Que dire de la "qualité" de cet oscillateur optique ?
L'oscillateur optique présente une résonance très aigue ( d'acuité bien supérieure à celle des autres oscillateurs ).
|
.
|
Puissance du laser, directivité.
Le laser utilisé en lycée est un laser hélium-néon de fréquence fHe-Ne de puissance P = 2 mW.
A
quelques centimètres de la sortie du laser, on mesure en interposant un
petit écran perpendiculairement au faisceau, une tache lumineuse de
diamètre 2 mm. Deux mètres plus loin, la tache s'est élargie et
présente un diamètre de 9 mm. En supposant que le rayon laser présente
un évasement conique, calculer un ordre de grandeur de la divergence du faisceau ( angle entre le rayon extrème et l'axe du faisceau ).
tan a ~ a = (0,5 *9 10-3) / 2 =2,25 10-3 ~2 10-3 rad .
Calculer la puissance surfacique ( puissance par unité de surface en W m2 ) du laser à l'intérieur de la tache de diamètre 2 mm.
pr2 = 3,14 * (10-3)2 = 3,1 10-6 m2 ; P /( pr2) =0,002 / (3,1 10-6) =6,4 102 W m-2,
c'est à dire du même ordre de grandeur que la puissance surfacique du
rayonnement solaire ressentie au niveau de la terre ( 1 kW m-2).
Dans certaines applications, le laser traverse, à sa sortie, un système qui a pour fonction d'élargir le faisceau.
Bien
que le faisceau laser soit très directif, cette divergence est encore
trop importante pour certaines expériences nécessittant un aller-retour
de la lumière sur de très longues distances.
Afin de comprendre
l'intérêt d'un élargissement du faisceau, une explication préalable de
la divergence naturelle du faisceau laser est indispensable. Pour cela,
on admet que cette divergence est liée à la diffraction du faisceau sur
ces propres bords. Cette explication, un peu simpliste, permet
néanmoins de bien appréhender le phénomène.
Quelle est l'ouverture angulaire q d'un faisceau de longueur d'onde l passant au travers une ouverture de dimension caractéristique d ?
q = l / d.
Calculer q. d = 0,36 mm. l = c / fHe-Ne = 3,00 108 / (4,74 1014 ) =6,33 10-7 m.
q = 6,33 10-7 / (0,36 10-3) = 1,8 10-3 rad, valeur du même ordre de grandeur que celle trouvée ci-dessus, d'où la pertinence de ce modèle. |
Rôle de l'élargisseur.
Pour des applications en télémétrie à grandes distances, cette divergence intrinsèque du faisceau est intolérable.
Lors d'une expérience en télémétrie entre la terre et la lune, distantes de D = 3,9 105 km environ, estimer
l'ordre de grandeur de la tache produite sur la surface lunaire par ce
laser s'il ne disposait pas d'élargisseur de faisceau.
Rayon de la tache circulaire : q D avec q = l/d =512 10-9 /(3,6 10-4)=1,42 10-3 rad ; puis 1,42 10-3 * 3,9 105 = 5,5 102 km.
Réduire
l'élargissement de la tache nécessite de diminuer la divergence
naturelle du faisceau. L'élargisseur permet d'accroître simplement
ladimension intrinsèque du faisceau laser. La caractéristique de ce
dispositif est son grandissement transversal g qui est simplement le rapport entre le diamètre du faisceau en sortie et le diamètre du faisceau en entrée.
Expliquer pourquoi l'ouverture du faisceau est censée diminuer si on utilise un élargisseur de faisceau.
La divergence naturelle du faisceau laser est due, d'après le modèle proposé, à la diffraction sur ces propres bords.
Or q = l / d ( sans élargisseur ) ; q' = l / (gd) = q / g ( avec élargisseur : g >1 ).
La divergence naturelle des faisceaux laser utilisés en télémétrie est de 2 10-5 rad. Calculer g.
g = q/q' ~ 2 10-3 / (2 10-5) ~1 102.
|
|