|
|
|
|
Cette
dernière question aborde le problème de la mesure des vitesses de
rotation, problème d'une grande importance dans le domaine de la
navigation inertielle. On peut citer notamment l'esemple des satellites
dont l'orientation est cruciale afin garantir elur bon fonctionement.
L'emploi du laser peut permettre de mesurer de faibles vitesses
angulaires et ansi de pouvoir détecter de petits mouvements de rotation.
Dans ledomaine de la navigation, ces dispositifs tendent d'aileurs peu àpeu à supplanter les gyroscopes mécaniques.
Effet Sagnac.
Cet
effet, découvert par Sagnac en 1914, permet de mesurer, par une
méthode optique, la rotation d'un référentiel par rapport à un
référentiel galiléen. L'analyse ci-dessous a pour objet de présenter
qualitativement cet effet puis de faire un calcul plus précis sur le
dispositif de la figure 10.
Schéma de principe.
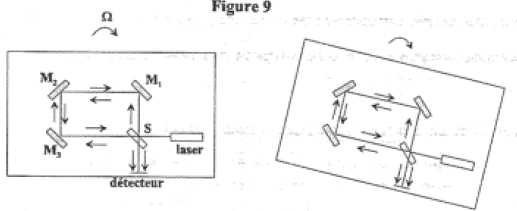
La
séparatrice S divise le faisceau laser en deux sous-faisceaux qui
circulent ainsi en contre-sens dans la boucle rectangulaire délimitée
par les miroirs M1, M2 et M3. Après un nouveau passage à travers S les faisceaux sont recombinés et analysés par le détecteur.
l'expérience montre qu'une rotation de vitesse angulaire W modifie l'enregistrement. La mesure associée à cette modification, permet de déterminer la valeur de la vitesse de rotation.
Aspect quantitatif.
On
considère un gyroscope à fibre optique à l'intérieur duquel des rayons
lumineux, produits par un laser de longueur d'onde égale à 633 nm, ne
sont pas guidés par des réflexions sur des miroirs mais sont canalisés
par des fibres optiques.
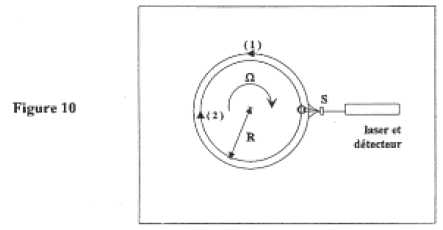
S
a pour rôle de diviser le faisceau laser en deux faisceaux circulant en
sens inverse. Après un tour, les signaux sont recombinés par S et
analysés par le détecteur. les raisonnements sont conduits dans le
référentiel du laboratoire R supposé galiléen, dans lequel la lumière
voyage à la vitesse c.
|
.
.
On considère les rayons lumineux entrant dans la fibre en O à l'insatnt t=0.
Morsque
le rayon 1 se propage, puisqu'il circule en sens inverse de la rotation
globale du dispositif, le trajet qu'il doit parcourir pour retrouver le
point O est, dans R, inférieur à un tour. Au contraire, le rayon 2 qui
circule dans le même sens que le sens de rotation global, parcourt,
dans R, un peu plus d'un tour avant d'atteindre à nouveau le
point O.
Montrer, qu'en bonne approximation, le décalage entre les deux temps de propagation pour revenir en O est 4AW / c2.
A représente l'aire de la surface de la boucle de l'instrument.
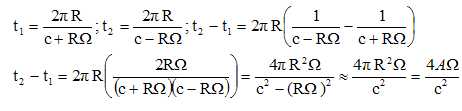
On
admettra que ce résultat se généralise à d'autres configurations
géométriques à condition que A représente l'aire de la surface de la
courbe férmée décrite par la lumière.
Ce décalage temporel est associé à une différence de trajet dL = c dt.
La capacité du détecteur à mesurer cette différence de trajet est liée
intrinsèquement à la longueur d'onde du rayonnement utilisé.
Calculer la plage des vitesses angulaires accessibles par cette méthode. A = 1 m2 ; dL supérieure ou égale à 1 nm.
dt = t2-t1 = dL/c ; c2 dt = 4AW ; c dL = 4AW ; W = c dL / (4A)
W =3,0 108 *10-9 /4) =7,5 10-2 rad/s.
On peut mesurer des vitesses de rotation supérieures ou égales à 0,075 rad/s.
Comment pourrait-on accroître les performances de ce dispositif ?
En augmentant A, on pourra mesurer des vitesses de rotation encore plus faibles.
|
|