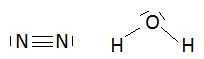|
|
|
|
Principal
constituant gazeux de l'atmosphère, le diazote est essentiel à la
détermination de certains paramètres thermodynamiques de celle-ci.
Introduction.
Ecrire les schémas de Lewis des molécules de diazote et d'eau. Préciser la géométrie de la molécule d'eau.
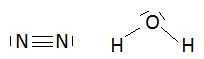
La molécule d'eau a la forme d'un V.
Enoncer la
règle de l'octet. Quels éléments obéissent bien à cette règle ? Dans
les molécule d'eau et de diazote, la règle de l'octet est-elle vérifiée
pour tous les constituants ?
Les
atomes ( de l'élément lithium ( Z=3) à l'élément chlore ( Z = 17)
ont tendance à compléter à huit leur couche électronique externe. Les
éléments azote et oxygène respectent cette règle dans les molécules
précédentes. L'élément hydrogène a tendance à compléter à 2 sa
couche électronique externe ( règle du duet ).
Utilisation du laser Lidar.
L'impulsion du laser est égale à t.
Si on considère deux molécules rétrodiffusant ( réflexion
vers l'arrière ) la lumière entre deux altitudes différentes, les échos
renvoyés par ces molécules sont séparés si la fin du signal renvoyé par
la molécule la plus proche du détecteur arrive avant le début de l'écho
dû à la molécule la plus éloignée.
Quelle est la valeur minimale de t qui permet une résolution en altitude de 30 m ?
t = 30 / (3 108) = 1,0 10-7 s.
Lors de sa propagation dans l'atmosphère, l'intensité lumineuse du faisceau laser suit l'équation :
d(I(z) / dz = -n(A) s(A, l) I(z). (1)
n(A) : nombre de moles du constituant A par unité de volume ;
s(A, l) est appelée section efficace d'absorption de l'espèce A pour la longueur d'onde l. s(A, l) s'exprime en m2 mol-1.Cette fonction présente un maximum très prononcé pour une ou plusieurs valeurs de l
connues pour chaque constituant atmosphérique. C'est ainsi que, en
travaillant avec un laser dont la longueur d'onde vaut précisément une
des valeurs caracétristiques précédentes, on peut s'assurer que
l'intensité du laser subit une variation essentiellement dominée par
l'espèce A.
Montrer qu'entre deux altitudes z1 et z2 relativement proches, on obtient :
ln ( I(z2) / I(z1)) = -n(A) s(A, l) ( z2-z1).
(1) s'écrit : d I(z) / I(z) = -n(A) s(A, l) dz ; d ln(I(z)) = -n(A) s(A, l) dz.
Intégrer entre les altitudes z1et z2.
ln I(z2) -ln I(z1) = ln ( I(z2) / I(z1)) = -n(A) s(A, l) ( z2-z1).
Pourquoi est-il important de travailler entre deux altitudes suffisamment proches ?
La pression diminue avec l'altitude ; le nombre de molécules constituant l'air diminue avec l'altitude.
Travailler entre
deux altitudes distantes de 500 m donnerait une composition moyenne et
non pas une cartographie de la teneur en eau en fonction de l'altitude.
Enfin
il ne faut pas que le signal réfléchi soit trop faible du fait de
l'absorption des photons par les molécules de l'atmosphère.
Les caractéristiques moléculaires de l'eau et du diazote font que s(H2O) passe par un pic pour l = 2730 nm et que s(N2) passe par un maximum à l = 4290 nm.
Dans quel domaine spectral se situent ces longueurs d'onde ?
Ces valeurs sont supérieures à 800 nm, elles appartiennent au domaine infrarouge.
|
.
Exploitation d'une expérience.
Afin
de sonder des altitudes différentes, on choisit d'analyser les échos
reçus à des instants précis dont on fait varier l'écart à l'aide d'un
détecteur muni d'un obturateur.
Etude à 2730 nm.
Une
impulsion lumineuse est émise dans l'atmosphère à la verticale de la
station à un instant choisi comme origine des temps. Des photons sont
notamment reçus aux instants t1 = 3,36 µs et t2 = 3,67 µs. Ces derniers proviennent de la diffusion de molécules d'eau à deux altitudes différentes notées z1 et z2.
Calculer ces altitudes. s(H2O) = 1,1 10-3 m2 mol-1.
z1 = 3 108 *3,36 10-6 / 2 = 504 m.
z2 = 3 108 *3,67 10-6 / 2 =550,5 m.
z2-z1 ~46,5 m.
En mesurant les intensités des signaux reçus à ces instats, on accède au rapport I(z2) / I(z1) qui vaut 0,425.
Calculer n(H2O) aux altitudes envisagées. s(H2O) = 1,1 10-3 m2 mol-1.
Cela constitue ainsi une estimation de la concentration moyenne en vapeur d'eau entre les altitudes z1 et z2 au moment de l'expérience.
ln ( I(z2) / I(z1)) = -n(A) s(A, l) ( z2-z1).
n(H2O) = -ln ( I(z2) / I(z1)) / (s(H2O, l) ( z2-z1)) = -ln 0,994 / (1,1 10-3 *46,5) =0,118 mol m-3.
Etude à 4290 nm.
Pour les mêmes valeurs de t1 et t2, I(z2) / I(z1) vaut 0,425.
Calculer n(N2) aux altitudes envisagées. s(N2) = 6 10-4 m2 mol-1.
Cela constitue ainsi une estimation de la concentration moyenne en diazote entre les altitudes z1 et z2 au moment de l'expérience.
n(N2) = -ln ( I(z2) / I(z1)) / (s(N2, l) ( z2-z1)) = -ln 0,425 / (6 10-4 *46,5) = 30,7 mol m-3.
|
|