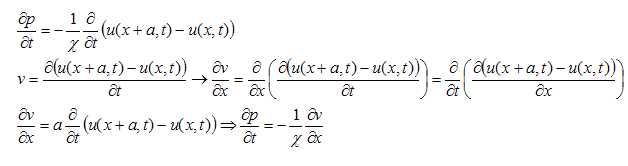|
|
|
|
Préliminaires.
Qu'appelle-t-on ondes mécaniques ? Quelle relation existe-t-il entre la fréquence n et la longueur d'onde l ?
On appelle onde mécanique progressive le
phénomène de propagation d'une perturbation
dans un milieu matériel sans transport de
matière, mais avec transport d'énergie. Une onde se propage, à partir de la source, dans
toutes les directions qui lui sont offertes.
La célérité "c" , exprimée en m s-1, est la vitesse de propagation de l'onde. C'est
le rapport entre la distance d (m) parcourue par l'onde et
la durée Dt (s) du
parcours. C'est une propriété du milieu de
propagationt.
l = c /n.
Définir ce qu'est une onde longitudinale et en donner un exemple. Faire de même pour une onde transversale.
Une onde est longitudinale lorsque le
déplacement des points du milieu de
propagation s'effectue dans la mêmehttp://www.chimix.com/pages/capes13.html direction
que celle de la propagation. L'onde sonore se propage dans les trois
dimensions de l'espace. Chaque point P vibre
longitudinalement dans la
direction de propagation du signal.
Une onde est transversale lorsque le
déplacement des points du milieu de
propagation s'effectue perpendiculairement à
la direction de propagation. Onde transversale à la surface de
l'eau : chaque point P de la surface se
soulève
verticalement puis
reprend sa place alors que les rides se
déplacent
horizontalement
à la surface de l'eau.
Définir ce qu'est une onde sonore en détaillant son principe physique de propagation.
Une
onde sonore est la propagation d'une modification ( variation ) de la
pression d'une colonne d'air. On observe périodiquement une alternance de surpression et dépression.
L'oreille humaine entend, en moyenne, des sons de fréquence comprise entre 20 Hz et 20 kHz.
Situer dans ce domaine spectral les sons graves et les sons aigüs.
Les sons graves ont des fréquences proches de quelques dizaines de hertz. Les sons aigus ont des fréquences élévées.
Quel est le rôle du tympan ?
Le tympan est une membrane située au fond du conduit auditif qui transmet les vibrations de l'air à la chaine des osselets.
Modèle de propagation du son dans l'air.
Pour
décrire la propagation d'une onde sonore longitudinale dans l'air, on
considère un système modèle représenté ci-dessous, et caractérisé par
les points suivants :
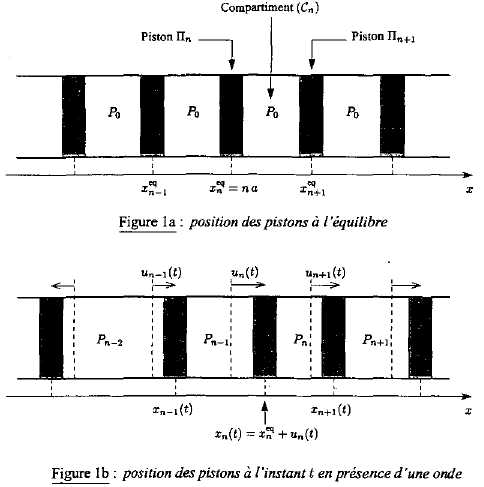
- Un tuyau rectiligne de section S est divisé
en une infinité de compartiments par des pistons rigides de masse m et
de section S. Le compartiment Cn correspond à l'espace compris entre les pistons Pn et Pn+1.
- Dans chaque compartiment se trouve une mole d'un gaz, assimilé à un gaz parfait.http://www.chimix.com/pages/capes13.html
- A l'équilibre, c'est à dire en absence d'onde sonore, l'abscisse du piston Pn est xnéq
= n a ; la pression et la température sont identiques dans chaque
compartiment ( équilibre mécanique et thermique ) et on les note
respectivement P0 et T0.
- Hors équilibre, c'est à dire lors du passage de l'onde sonore, labscisse du piston Pn vaut xn = n a + un(t) à l'instant t et la pression dans le compartiment Cn vaut Pn.
On
suppose que l'évolution de la mole e gaz dans chaque compartiment se
fait suivant la loi de Laplace : l pression P dans le
compartiment est reliée à son volume V par : PVg=constante, où g est une constante appelée coefficient polytropique de Laplace.http://www.chimix.com/pages/capes13.html
|
Surpression sonore.
Etablir l'expression de la pression Pn en fonction de P0, g a, un et un+1.
A l'équilibre, volume du compartiment Cn : V0 =S(xn+1éq-xnéq) =S((n+1a-na) = S a ; pression du gaz P0.
De même, hors équilibe : Vn =S(xn+1-xn) =S(xn+1éq+ un+1(t) -xnéq-un(t)) = S( a + un+1(t)-un(t)) ; pression du gaz Pn.
Loi de Laplace : P0V0g =PnVng = P0(Sa)g =Pn(S( a + un+1(t)-un(t)))g ; P0ag =Pn( a + un+1(t)-un(t))g.
P0 =Pn( 1 +( un+1(t)-un(t)) / a )g ; Pn = P0( 1 + (un+1(t)-un(t)) / a)-g.
Dans l'approximation de l'acoustique linéaire, |un(t)| << a pout tout n.
Montrer
que l'expression précédente s'écrit : Pn-P0 = -1/c(un+1-un)/a. (1+e)µ ~1+µe si e <<1.
Pn ~ P0( 1 -g (un+1-un) / a) ; Pn - P0 ~ -P0 g (un+1-un) / a.http://www.chimix.com/pages/capes13.html
Donner l'expression de la constante c. Son signe est-t-il en accord avec le "sens physique" donné à cette grandeur ?
c =1/( P0 g).
En cas de surpression : Pn - P0 >0, un+1-un <0, a >0 d'où c =1/( P0 g) positif.
La constante c est appelée coefficient de compressibilité. Donner sa dimension et justifier son nom.
g est sans dimension, c a la dimension de l'inverse d'une pression ( pa-1).
La compression d'un gaz est d'autant plus difficile que la pression est plus grande.
Que vaudrait c si le gaz était incompressible ? Vérifier qu'aucune onde ne se propagerait dans ce cas.
c serait très grand et Pn=P0 : sans variation de pression du gaz, aucune onde sonore ne peut se propager.
Equation discrète de propagation.
La force de pression qu'exerce un gaz à la pression P sur un piston de section S est donnée en module par la relation F = PS.
Faire une figure représentant les actions horizontales s'exerçant sur le piston Pn. On négligera les frottements.http://www.chimix.com/pages/capes13.html
En appliquant la deuxième loi de Newton au piston Pn obtenir l'équation différentielle du mouvement. r0 = m/(aS) : masse volumique du milieu.

Justifier la dimension de c.
1/c
est une pression, soit une force / surface ; une force est une masse
fois une accélération soit une masse fois une longueur divisée par le
carré d'un temps. 1/c s'exprime en : kg m-1 s-2.
1/r0 est un volume massique soit m3 kg-1. Par suite c2 s'exprime en m2 s-2 ; "c" est donc une vitesse.
|
Approximation des milieux continus et équation de d'Alembert.
L'approximation des milieux continus revient à prendre "a" très petit devant la longueur d'onde l caractéristique de l'onde sonore.
un+1(t) = u(na+a,t) = u(x+a, t) ; un-1(t) = u(na-a,t) = u(x-a, t).
Pour une fonction f de la variable y, il est possible d'écrire le développement au voisinage de y.
f(y+e) ~ f(y) + e df(y)/dx + ½e2 d2f(y)/dy2 si |e| est petit devant 1.
Pour t constant : u(x+a, t) ~ u(x,t) + adu(x,t)/dx +½a2d2u(x,t)/dx2.
u(x-a, t) ~ u(x,t) - adu(x,t)/dx +½a2d2u(x,t)/dx2.
u(x+a, t) +u(x-a, t) -2u(x,t) =a2d2u(x,t)/dx2.
Par suite d2u(x,t)/dt2 = c2d2u(x,t)/dx2 soit : d2u(x,t)/dx2 -1/c2 d2u(x,t)/dt2 =0. ( éq dite d'Alembert ).
Solutions en ondes progressives de cette équation.
Les solutions de cette équation se mettent sous la forme u(x,t) = f(x-ct) +g(x+ct).http://www.chimix.com/pages/capes13.html
Vérifier que u(x,t) obéit à l'équation d'Alembert.
du(x,t)/dt = -c df(x-ct)/dt +c dg(x+ct)/dt.
d2u(x,t) /dt2 = c2d2f(x-ct)/dt2 +c2 d2g(x+ct)/dt2.
-1/c2 d2u(x,t)/dt2 = -d2f(x-ct)/dt2 - d2g(x+ct)/dt2.
du(x,t)/dx = df(x-ct)/dx + dg(x+ct)/dx.
d2u(x,t) /dx2 =d2f(x-ct)/dx2 + d2g(x+ct)/dx2.
L'équation d'Alembert est bien vérifiée.
Rappeler la définition d'une onde progressive à une dimension.
On appelle onde mécanique progressive le phénomène de propagation d'une
perturbation dans un milieu matériel sans transport de matière, mais avec
transport d'énergie.
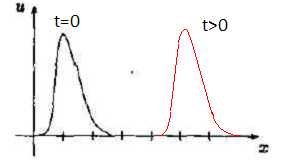
Dans
cette question, on prend la fonction g identiquement nulle. La figure
suivante donne une allure de la fonction u(x,t) = f(x-ct) à l'instant
t=0.
Représenter l'allure de u(x,t) en fonction de x, pour t >0.
 http://www.chimix.com/pages/capes13.html http://www.chimix.com/pages/capes13.html
La
fonction f(x-ct) représente une onde progressive à une dimension de
céléritéc, se propageant dans le sens des x positifs.
g(x+ct)
représente une onde progressive de célérité c se propageant dans
le sens des x négatifs. La solution générale représente deux ondes qui
peuvent " se croiser sans se perturber". |
Impédance acoustique.
Soit v(x, t) =du/dt
la vitesse du gaz en x à l'instant t. De plus, on note p(x, t) la
pression en x à l'instant t dans le milieu : p(x,t) = P(x,t)-P0 représente la surpression par rapport à l'équilibre.
On définit l'impédance acoustique Z ( ou résistance acoustique ) du milieu parcouru par une onde progressive par p = Z v.
Justifier cette définition en évoquant une analogie électrique.
A la vitesse dx/dt correspond l'intensité i = dq/dt.
A une variation de pression correspond une différence de potentiel U ; or U = R i, par analogie p = Z v.
Montrer que :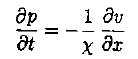 http://www.chimix.com/pages/capes13.html http://www.chimix.com/pages/capes13.html
Pn - P0 ~ -1/c (un+1-un) / a ; p(x,t) =P(x,t)-P0 =-1/c (u(x+a, t)-u(x, t)) / a.
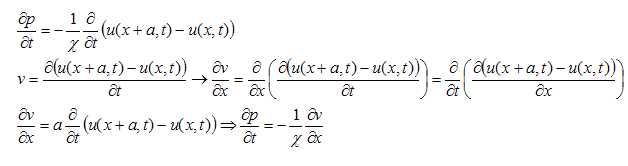
Pour une onde progressive de la forme f(x-ct), en déduire que Z = r0 c.
Pour une onde progressive de la forme g(x+ct), en déduire que Z = - r0 c.
A.N pour l'air : g = 1,4 ; r0 = 1,19 kg m-3 ; P0 = 1,01 105 Pa ; M(air) = 29 g/mol ; R = 8,32 J mol-1 K-1.
T0 =P0V0 / R = P0M / (Rr0 )=1,01 105*0,029 / (8,32 *1,19) = 295,8 ~296 K ou 23°C.
c =1/( P0 g) =1/(1,01 105*1,4) =7,07 10-6~ 7,1 10-6 pa-1.
c = (1/(c r0)½ = (1 / (7,07 10-6*1,19))½ =344,7 ~345 m s-1.
Zair = r0 c =1,19 * 344,7 ~ 410 kg m-2 s-1.
Commenter, à l'aide des résultats du modèle, les valeurs expérimentales suivantes de la célérité du son dans l'air :
Les valeurs obtenues à l'aide du modèle sont en accord avec les valeurs expérimentales.
|
Discussion de la validité de quelques hypothèses.
L'hypothèse de l'air assimilé à un gaz parfait est-elle plausible pour les pressions faibles ou élevées ? Justifier.
Pour les faibles pressions ( peu d'interactions entre molécules du gaz ), on peut assimiler l'air à un gaz parfait.
Au
lieu d'utiliser la loi de Laplace, on aurait pu prendre l'hypothèse
antérieure de Newton : la propagation du son est isotherme, c'est à
dire que la température reste égale à T0 lors du passage de l'onde.
Montrer que cette hypothèse revient à faire tendre g vers 1 et en déduire la valeur de la célérité du son dans l'air à 25 °C dans cette hypothèse. Conclure.
P0 V0 = PV = RT0 = constante, soit g = 1.
c ==1/( P0 g) =1/(1,01 105*1) =9,90 10-6 pa-1.
c = (1/(x r0)½ = (1 / (9,90 10-6*1,19))½ ~291 m s-1, valeur trop éloignée de la valeur expérimentale.
L'hypothèse de Newton n'est pas satisfaisante.
|


 http://www.chimix.com/pages/capes13.html
http://www.chimix.com/pages/capes13.html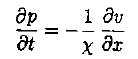 http://www.chimix.com/pages/capes13.html
http://www.chimix.com/pages/capes13.html