|
|
|
|
On
considère une bouilloire électrique contenant Veau
= 800 mL d’eau.
On étudie le système {eau}.
La température initiale Ti du système est de
20°C. On met ensuite la bouilloire en fonctionnement jusqu’à atteindre
une température finale Tf = 70°C.
Exprimer
la variation d’énergie interne de l’eau lors de cette transformation de
façon littérale, en fonction des données de l’énoncé. Faire
l’application numérique.
Données : Capacité calorifique massique de l’eau : ceau
= 4,18.103 J.kg-1.°C-1
Masse volumique de l’eau : ρeau = 1,0 kg.L-1.
DU
=Q = Veau reau
ceau(Tf-Ti)
=0,800 *1,0 *4,18 103 (70-20)=1,672 105
~1,7 105 J.
La bouilloire remplie d’eau chaude à la température Tf
est placée dans une pièce où la température notée Text
vaut 20°C.
Sachant que l’expression générale du flux thermique ϕ à travers une
paroi de résistance thermique Rth où la
température de part et d’autre vaut T1 et T2
est : F =
Q/Dt =|T2-T1| /Rth
; on rappelle aussi que le flux thermique correspond à l’énergie
thermique échangée Q pendant l’intervalle de temps Δt.
Donnée : Rth(bouilloire) = 0,17 K.W-1.
Calculer
le flux thermique qui traverse la paroi de la bouilloire.
Q = (70-20) / 0,17 = 2,941 102 ~2,9 102
W.
Compléter
le schéma en représentant le sens du transfert thermique
correspondant à ce flux ϕ.
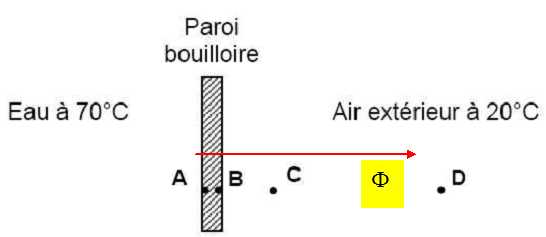
En
considérant la température de l’eau constante, en déduire l’énergie
thermique Q transférée à travers les parois pendant 2 minutes.
Q = FDt =
294,1*2*60=3,53 104 ~3,5 104
J.
Quel
est le mode de transfert thermique majoritaire :
• entre A et B ? Conduction.
• entre C et D ? Convection.
|
.
|
On
cherche à diviser le flux thermique par cinq. Pour cela, on accole à la
paroi de la bouilloire de surface 0,12 m² une couche d’isolant mince de
même surface. On considère alors que la bouilloire et l’isolant mince
constituent un assemblage de parois planes.
On admet aussi que la résistance thermique Rth
d’un matériau d’épaisseur e, de conductivité thermique λ et de surface
S peut être donnée par la relation suivante :
Rth = e/(lS)
Donnée : conductivité thermique de l’isolant : λisolant
= 0,04 W.m-1.K-1.
Sachant que les résistances thermiques s’additionnent dans le cas de
parois accolées, calculer
l’épaisseur d’isolant qui permettra de diviser le flux thermique par
cinq. On donnera expression littérale et valeur numérique
de l’épaisseur e.
Résistance thermique de la bouilloire isolée thermiquement :
Rtotale =Rth(bouilloire)
+ e / (lisolant
S).
Flux thermique : F' = |T2-T1|
/Rtotale
=F / 5.
[Rth(bouilloire)
+ e / (lisolant
S)] * 0,2 F =|T2-T1|
Rth(bouilloire)
+ e / (lisolant
S) =5|T2-T1|
/F.
e
/ (lisolant
S) =5|T2-T1|
/F-Rth(bouilloire)
e = [ 5|T2-T1|
/F-Rth(bouilloire)
](lisolant
S).
e = [5*50 / 294,1 -0,17)*0,04*0,12 =3,3 10-3 m =
3,3 mm..
|
|