|
|
|
|
Un
parachutiste expérimenté a le projet de s’élever à une altitude de 40
km au moyen d’un ballon sonde gonflé à l’hélium. Arrivé à cette
altitude, il envisage de sauter de la capsule du ballon pour effectuer
un saut, d’abord en chute libre, avec l’ambition de battre un record de
vitesse, puis en parachute afin de regagner la terre ferme en douceur.
Effectuer tous les calculs en ne conservant que trois chiffres
significatifs dans les résultats.
A.
Décollage.
On suppose qu’au décollage le système {ballon+capsule+sauteur}, étudié
dans un référentiel terrestre considéré galiléen, n’est soumis qu’à son
poids et à la poussée d’Archimède.
Soit m : masse du sauteur et de son équipement, m’ : masse de la capsule, m’’ : masse du ballon.
V : volume du ballon ; ρ : masse volumique de l’air au sol ; g : accélération de la pesanteur au sol
On donne : m’+m’’= 750 kg ; V = 800 m3 ; ρ = 1,20 kg.m-3 ; g = 9,81
m.s-2.
Calculer la valeur de la poussée d’Archimède FA, s’exerçant sur le
ballon au sol. On rappelle que FA = ρgV.
FA = ρgV = 1,20 *9,81 *800 =9417,6 ~9,42 103 N.
Calculer le poids P1 de l’ensemble {ballon+capsule}.
P1 = (m'+m")g =750*9,81 =7357,5 ~7,36 103 N.
On note P2 le poids du sauteur et de son équipement.
Ecrire la
relation fondamentale de la dynamique (2è loi de Newton) appliquée à
l’ensemble {ballon+capsule+sauteur et équipement}.
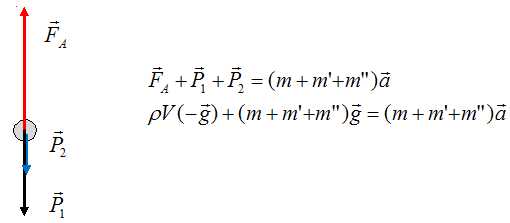
Etablir l’expression littérale de la relation que doit vérifier la
masse m pour réussir le décollage, en fonction de m’, m’’, ρ et V. En
déduire la valeur de cette masse, notée m*, qui ne doit pas être
atteinte.
La poussée doit être supérieure au poids total : rVg >(m+m'+m")g ; rV > m+m'+m" ;
m* = rV-m'-m" = 1,2 *800 -750 =210 kg.
|
.
|
B. Saut depuis la capsule.
Le
parachutiste se trouve maintenant à une altitude H = 40 km. On suppose,
dans toute cette partie B, la poussée d’Archimède sur le sauteur
négligeable. D’autre part, par commodité, on désigne simplement par «
le sauteur », l’ensemble constitué du sauteur et de son équipement, le
tout de masse m = 100 kg.
Etablir l’expression littérale de la force de gravitation Fg subie par le sauteur en fonction de m, de la constante de gravitation G, de la masse de la terre MT, du rayon de la terre RT, et de l’altitude H. On a alors Fg = P, P = m gH étant le poids du sauteur à l’altitude H.
Fg = GMTm/(RT+H)2.
Calculer gH avec H = 40 km ; G = 6,67 10-11 SI, MT = 5,97 1024 kg, RT = 6,37 106 m.
Fg = GMTm/(RT+H)2 = mgH ;
gH = GMT/(RT+H)2 =6,67 10-11 *5,97 1024 / (6,37 106 + 4,0 104)2 =9,69 m s-2.
Le
sauteur s’élance de la capsule sans vitesse initiale. On suppose qu’il
n’est soumis qu’à son poids P. On choisit un axe vertical z orienté
positivement vers le bas dont l’origine est la capsule. Ecrire la relation fondamentale de la dynamique appliquée au centre de gravité du sauteur.
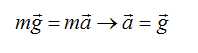
On suppose l’accélération de la pesanteur constante égale à gH dans les 2 questions suivantes.
Etablir la relation donnant la vitesse v du sauteur en fonction du temps t, soit v = f1(t), et l’appliquer en calculant la vitesse vL atteinte après 30 s de chute, exprimée en m.s-1 et en km.h-1.
La vitese est une primitive de l'accélération ; la vitesse initiale étant nulle, la constante d'intégration est nulle : v = gHt.
vL = 9,69*30 =281 m/s ou 281*3,6 = 1,01 104 km/h.
Etablir la relation donnant le déplacement z du sauteur en fonction du temps t, soit z = f2(t), et l’appliquer en calculant la distance parcourue h après 30 s de chute.
La position est une primitive de la vitesse. z = ½gHt2 + constante.
La constante d'intégration est nulle si l'origine de l'axe est au point de départ du saut.
h = 0,5*9,81*302 =4,41 103 m.
.
|
|
A
2 km d’altitude, le sauteur, se déplaçant maintenant dans les couches
denses de l’atmosphère, déclenche son parachute. Il est soumis en plus
de son poids à une force de frottement dont l’unique composante est sur
z et vaut Ff = -kv2. Le centre de gravité du sauteur obéit alors à l’équation mg – kv2 = m dv/dt.
Déterminer,
par analyse dimensionnelle, l’unité du coefficient de frottement k.
Calculer la valeur du coefficient de frottement k pour obtenir une
vitesse limite du sauteur vlim = 5 m.s-1.
mg – kv2 = m dv/dt. Chaque terme a la dimension d'une masse fois une accélération, soit M LT-2.
[v2]=L2T-2. [k] =M LT-2L-2T2 = ML-1.( kg m-1).
Lorsque la vitesse limite est atteinte dvlim/dt = 0 et k = mg / v2lim =100*9,81 / 25 = 4*9,81 = 39,2 kg m-1.
|
|